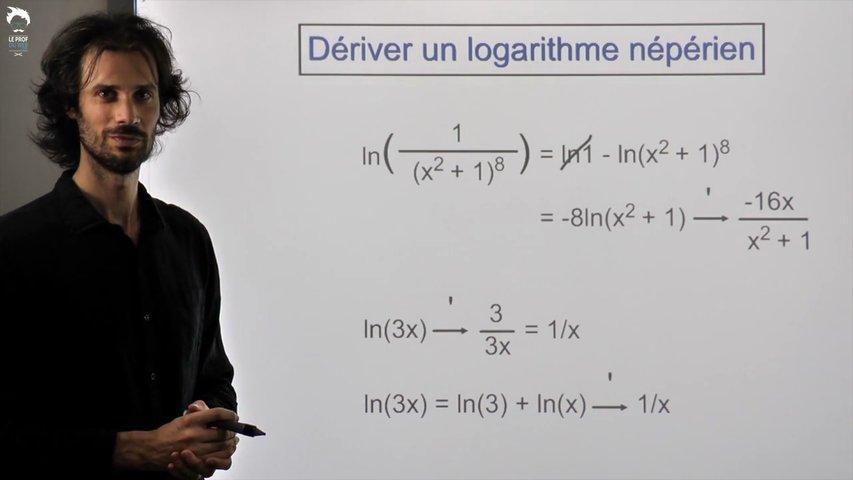MA

03  Dérivation
Une étude de fonction commence presque toujours par un calcul de dérivée.
S’il est faux, les questions suivantes aussi, et c’est souvent deux ou trois points partis en fumée…
La dérivée, c’est donc le calcul à ne pas planter dans un devoir.
En plus, en seconde partie d’année, sont étudiées les primitives, qui nécessitent de prendre les formules de dérivées « à l’envers ».
Bref, en Terminale, il faut maîtriser la dérivation sur le bout des doigts sinon toutes tes études de fonctions vont se transformer en parcours du combattant.
Heureusement, bonne nouvelle,il y a une seule vraie nouveauté en Terminale sur le sujet : la dérivée de composée.

01
Rappels et Nouveautés.

Rappel de l’essentiel et zoom sur la nouveauté : la dérivée de composée.
Les bases pour bien démarrer.
Une idée à garder en tête: le plus important, c'est en général de reconnaître la "forme globale".

 
01
Reconnaître une composée de fonctions
2 min 35 s Voir la vidéo

Assez simple

03 Reconnaître une composée de fonctions METHODE – RECONNAISSANCE DES COMPOSEES

Une vidéo pour éviter une erreur fatale !
Comme vous n’avez pas appris la composition en Première,
beaucoup d’entre vous ne reconnaissent pas les composées
et les prennent pour des produits.
La dérivée est alors fausse et avec elle tout le début de l’étude de fonction…
Un petit problème de vision qui coûte très cher.
2 min pour apprendre à reconnaitre la forme globale d’une dérivée et ne plus faire cette erreur…

02
Dériver des exponentielles et des logarithmes

Exponentielle et logarithme sont les nouvelles fonctions étudiées en Terminale.
Elles sont l’objet de la plupart des études de fonctions.
Il faut donc absolument être sûr de soi quand on les dérive.
D’autant plus que c’est très simple quand on a compris la méthode.
 
01

03
Tableaux de variations

Le but principal de la dérivation, c’est la construction de tableaux de variations.
Je te propose de revoir les tableaux de variations les plus classiques de Première.
À maîtriser au plus tôt en Terminale. 
01
Tableau de variations d'un polynôme de degré 3
3 min 4 s Voir la vidéo

D'un bon niveau

01 Tableau de variations d'un polynôme de degré 3

On monte d'un petit cran en difficultés avec le tableau de variations d'un polynôme de degré 3. Il faut se souvenir de la méthode pour trouver le signe d'un polynôme de degré... 2 ! En cas de doute à ce sujet, regarde ces deux vidéos :
- Racines et tableaux de signes d'un polynôme 1
- Racines et tableaux de signes d'un polynôme 2
Et si tu ne connais pas la "technique de l'indien", elle est expliquée ici Technique de l'indien

Etude d’un polynôme de degré 2
5 min 3 s Voir la vidéo

D'un bon niveau

03 Etude d’un polynôme de degré 2

On construit le tableau de variations d'un polynôme de degré 2 puis on calcule les équations de deux de ses tangentes.
On voit enfin comment utiliser les tangentes pour faire un tracé précis de la courbe.
Un exercice classique à maîtriser absolument !
En cas de difficultés je te propose trois vidéos :
Une vidéo pour savoir comment trouver le signe d'une fonction affine.
Une autre pour comprendre la formule qui donne l'équation d'une tangente.
Et une troisième pour réussir ses tracés de droite.

04
Dérivation et lecture graphique

Point méthode à voir absolument avant un devoir.
Deux vidéos qui présentent des questions plutôt simples mais que vous sautez en devoir,
parce qu’elles vous surprennent et que vous ne savez pas comment les prendre.
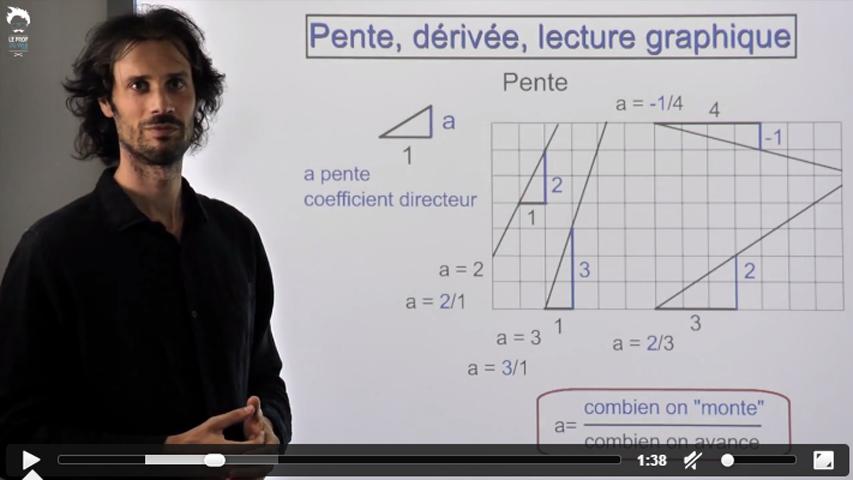
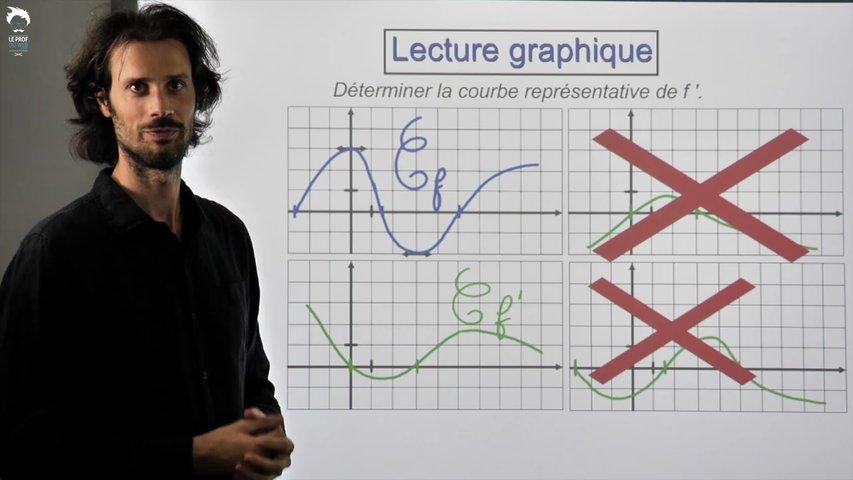
Leur point commun : ce sont des problèmes où la clef est dans la traduction.
Il faut savoir passer du graphique à une formule et vice-versa.

 
01
Rappel sur la notion de pente
6 min 5 s Voir la vidéo

Assez simple

01 Rappel sur la notion de pente METHODE – INTERPRETATION GRAPHIQUE DE LA DERIVEE – PENTE DE LA TANGENTE

En Terminale, vous avez tellement l’habitude d’utiliser la dérivée pour construire des tableaux de variations que vous finissez par croire qu’elle ne sert qu’à ça.
La dérivée en un point, c'est aussi la pente de la tangente à la courbe, un aspect géométrique de la dérivée essentiel dans de nombreux sujets de Bac !
Si tu as besoin de remettre tes idées au clair sur les tracés de droite et la notion de pente (ou coefficient directeur), regarde cette vidéo et les deux suivantes.

Lecture graphique dans une étude de fonction
5 min 7 s Voir la vidéo

Assez simple

02 Lecture graphique dans une étude de fonction PENTE DE LA TANGENTE – RECONNAITRE LA COURBE DE LA DERIVEE - QUESTIONS D’INTERPRETATION GRAPHIQUE - METHODE

Deux exercices classiques au bac où la dérivée ne sert pas à construire un tableau de variation.
Regarde cette vidéo de méthode pour ne pas te faire surprendre par ces questions un peu inhabituelles.
Il s’agit de :
- Trouver l’expression d’une fonction à partir d’informations sur sa courbe.
- Toujours à partir d’une courbe trouver la courbe de la dérivée parmi plusieurs courbes au choix.
Un classique des QCM.
Tu peux te préparer aux interprétations graphiques en regardant cette série de vidéos :
La dérivation : à quoi ça sert ?
Dérivée en un point, taux d'accroissement et tangente
Que faire quand la pente d'une droite ne tombe pas juste ?

05
Étude de signes

Parfois, souvent même, ce n’est pas le calcul de la dérivée qui vous pose le plus de problèmes mais l’étude de signe qui suit.
Deux vidéos de méthode centrées spécialement sur cette question qui n’est pas si simple car on va le voir, la méthode à appliquer change en fonction de l’expression.
Il faut donc savoir d’abord choisir la bonne méthode avant de l’appliquer.
01
Tableau de signes d'une expression 1/2
2 min 25 s Voir la vidéo

D'un bon niveau

01 Tableau de signes d'une expression 1/2 METHODE - CHOIX DE LA TECHNIQUE

Pour étudier le signe d'une expression, tu dois d’abord savoir quelle méthode appliquer.
Dans cette première partie nous expliquons comment choisir la bonne méthode sans perdre de temps.
Remarques: certaines méthodes sont découvertes en cours d'année de Terminale
donc pas de panique si tu ne comprends pas tout en début d'année.
Enfin, si tu veux revoir comment étudier rapidement le signe d’une fonction affine,regarde cette vidéo.
Et pour le signe d’un polynôme cette vidéo et la suivante.

06
Dériver une « puissance négative » ou un quotient avec une puissance au dénominateur

Plutôt rare en DS ou au bac.
Par contre, classique dans une interro de cours sur la dérivée.

 
01
Dériver efficacement une fonction de type 1 / x ^ n
4 min 35 s Voir la vidéo

D'un bon niveau

01 Dériver efficacement une fonction de type 1 / x ^ n CALCUL DE DERIVEE – PUISSANCE NEGATIVE – QUOTIENT AVEC PUISSANCES

Les puissances négatives de type « un sur x puissance n » ou plus généralement les quotients avec une puissance au dénominateur sont rarement l’objet d’étude de fonctions.
On peut néanmoins vous demander de les dériver pour une interro de leçon sur la dérivée ou dans un QCM.
On y voit deux méthodes.
La deuxième, la plus rapide, vous sera aussi indispensable dans le chapitre sur les Primitives.