11  Les probabilités continues

L’idée de calculer des probabilités avec des intégrales peut paraitre surprenante voire effrayante.
Pourtant comme tu vas le découvrir à travers ces vidéos
avec quelques schémas bien choisis
et deux fonctions de la calculatrice,
on peut comprendre et résoudre à peu près tous les exercices.
Entre trois et cinq points au bac sur ce chapitre où les questions sont assez prévisibles.
Des points assez facile à prendre avec un peu de méthode.

En pratique dans les devoirs et au bac vous êtes interrogés sur trois lois :
-    Uniforme
-    Exponentielle
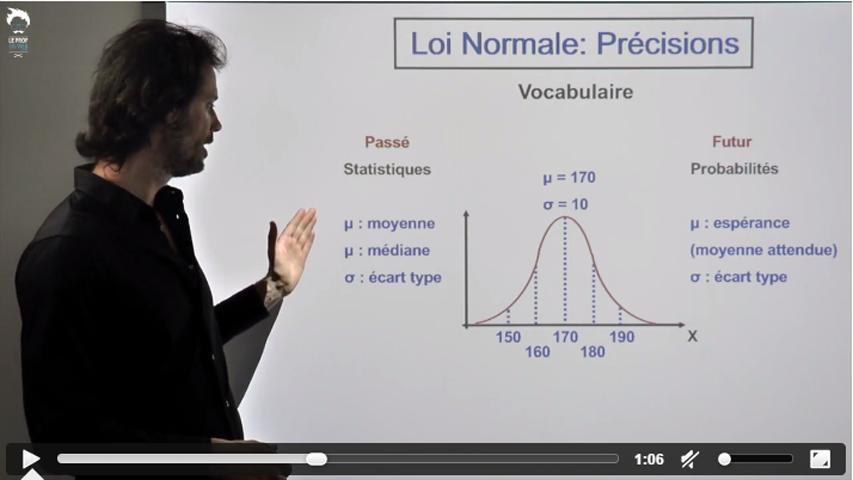
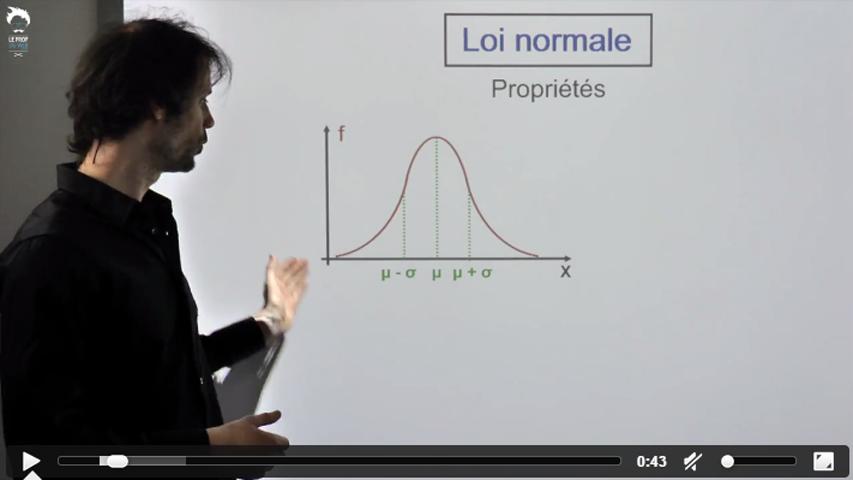
-    Normale
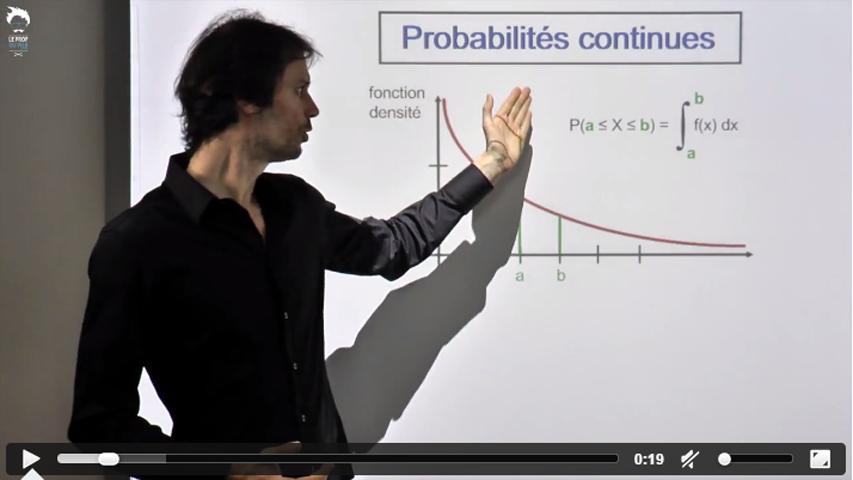
On présente ici des propriétés générales des probabilités continues
valables en particulier pour ces trois lois.

Première des trois lois au programme.
C’est de très loin la plus simple.
Trois vidéos pour être sûr de la maitriser.

Une loi qui donne lieu à des calculs intégrales avec des primitives…
mais toujours les mêmes !
Avec un peu d'entraînement tu connaitras par cœur les étapes et les résultats. 
Après le cours tu trouveras deux problèmes types
pour faire un tour complet des questions qui t’attendent.
Le seul point un peu plus difficile est la propriété "sans vieillissement".
Ça vaut la peine de s'entraîner à la redémontrer.
C’est souvent demandé en devoir.

Cette fois, les fonctions mathématiques sont trop compliquées pour mener à des calculs de primitives.
Mais c'est une bonne nouvelle
car tout va pouvoir se faire avec des schémas et la calculatrice.

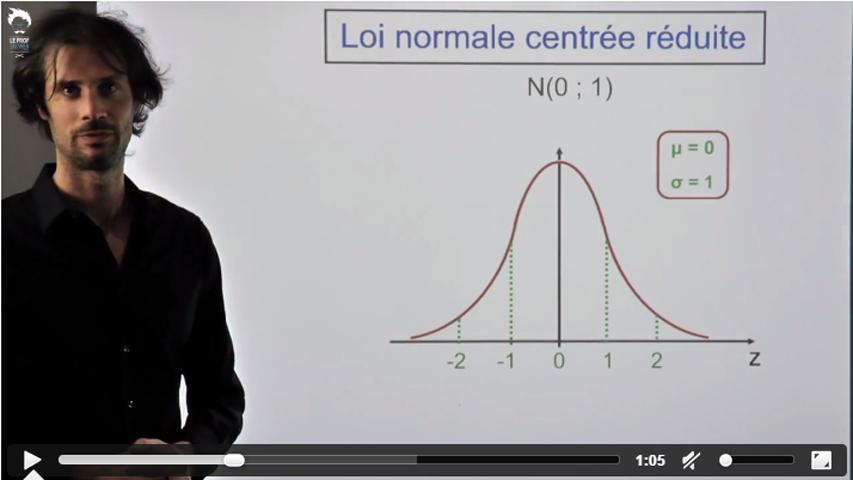
Cette loi en elle-même est très simple comme tu vas le voir dans la première vidéo
mais elle donne lieu à des exercices très techniques avec un changement de variable.
Ce sont les exercices durs du chapitre.
Ils sont difficiles parce qu'abstraits a priori.
Mais une fois de plus dans ce chapitre, ils sont stéréotypés donc prévisibles.
Il suffit d’apprendre la méthode et les étapes.
Un dernier effort si tu veux prendre tous les points dans les problèmes sur ce chapitre.