On commence ... par le commencement : traduire un problème concret pour l'écrire comme un système d'équations. On voit ensuite les deux méthodes pour le résoudre : substitution et combinaison linéaire. Enfin, on s'entraîne sur une série d'exemples.
Cette fois, on aborde les systèmes autrement.
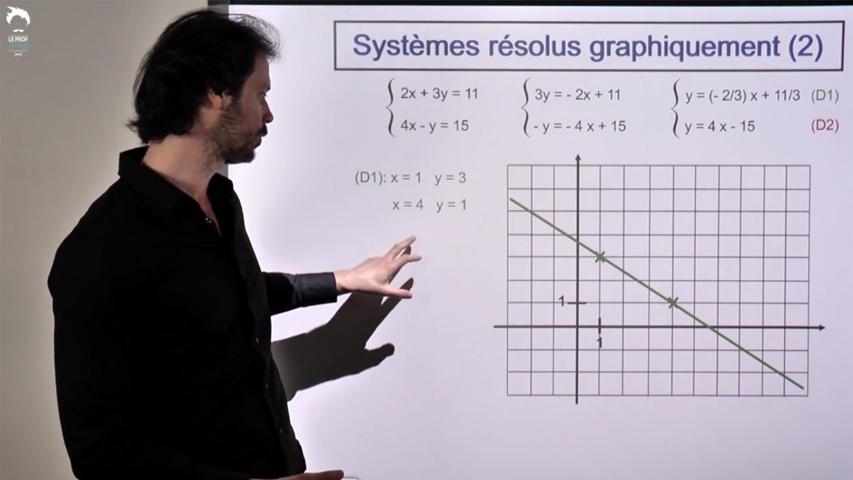
On trace des droites et on observe les solutions.
La méthode est plutôt fastidieuse. C'est surtout un moyen de comprendre ce qui se passe quand il n'y a pas une solution, mais aucune ou une infinité.
On y croise au passage pour la première fois une nouvelle écriture des droites appelée " équation cartésienne ".
Et cette idée clef à retenir : deux droites parallèles ont même pente !
On présente d'abord l'essentiel du chapitre, ce qu'il faut retenir et savoir faire.
Et puis je te propose deux problèmes que tu pourrais avoir en DS.