5 min 14 s
5 min 14 s
5 min 51 s
Le casse-tête du chapitre.
Un classique des DS sur lequel il faut s'entrainer.
Le tracé d'une fonction comportant deUX valeurs absolues.
de nombreux conseils pour gagner du temps...
Là encore, si tu ne te sens pas au top sur les Tracés de droites, ces deux vidéos devraient t'aider
- Comment tracer une droite sur un graphique ?
- Que faire quand la pente d'une droite ne tombe pas juste ?
6 min 5 s
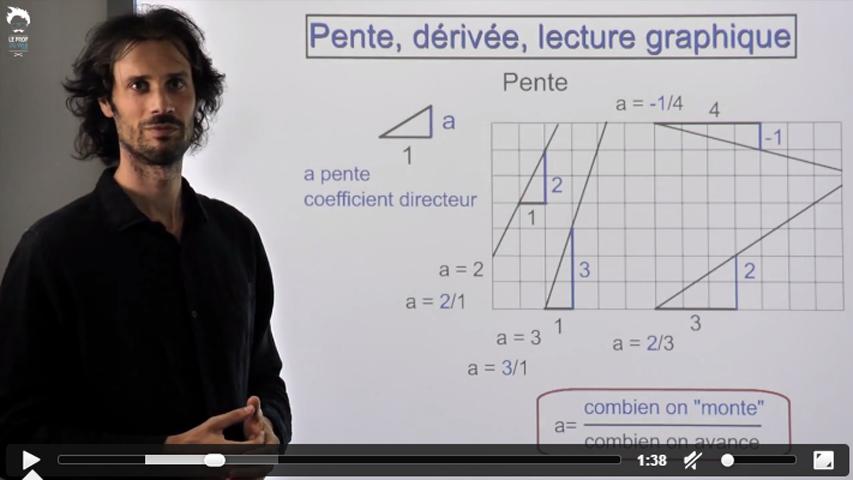
En Terminale, vous avez tellement l’habitude d’utiliser la dérivée pour construire des tableaux de variations que vous finissez par croire qu’elle ne sert qu’à ça.
La dérivée en un point, c'est aussi la pente de la tangente à la courbe, un aspect géométrique de la dérivée essentiel dans de nombreux sujets de Bac !
Si tu as besoin de remettre tes idées au clair sur les Tracés de droite et la notion de pente (ou coefficient directeur), regarde cette vidéo et les deux suivantes.
3 min 36 s
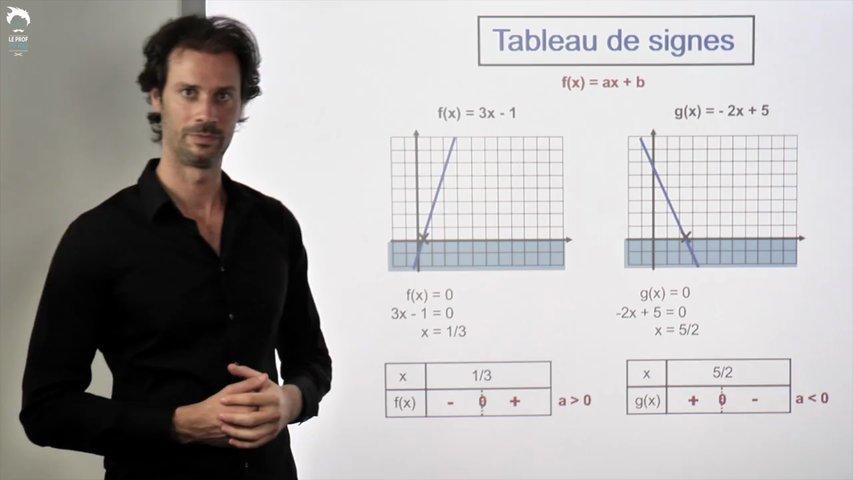
Dans les études de fonctions, il y a presque toujours des études de signes avec un, deux ou trois tableaux de signes de droites à faire. Autant apprendre à bien gérer ce problème tout de suite.
Ultra classique !
Niveau de maîtrise à viser proche du réflexe comme pour les lectures et Tracés de droites.
5 min 14 s
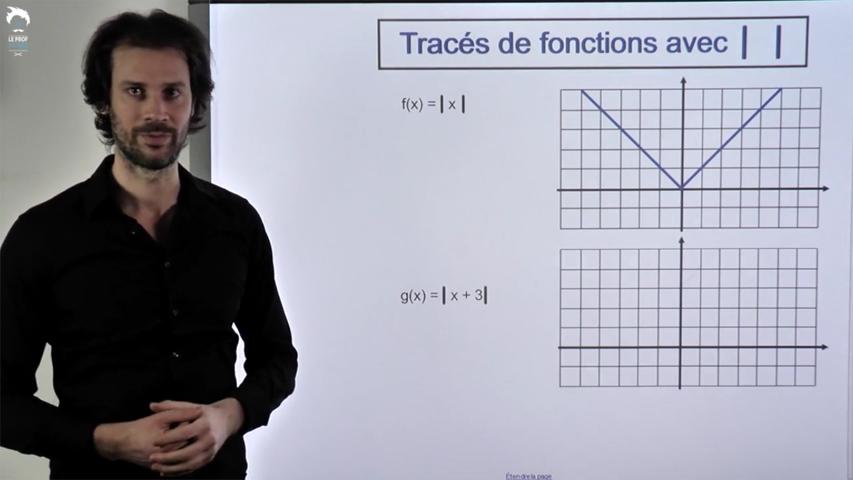
On voit comment tracer des fonctions comportant une valeur absolue.
La clef: travailler par "zone".
Si tu te sens un peu rouillé avec les Tracés de droites, revois ces deux vidéos :
- Comment tracer une droite sur un graphique ?
- Que faire quand la pente d'une droite ne tombe pas juste ?
4 min 13 s
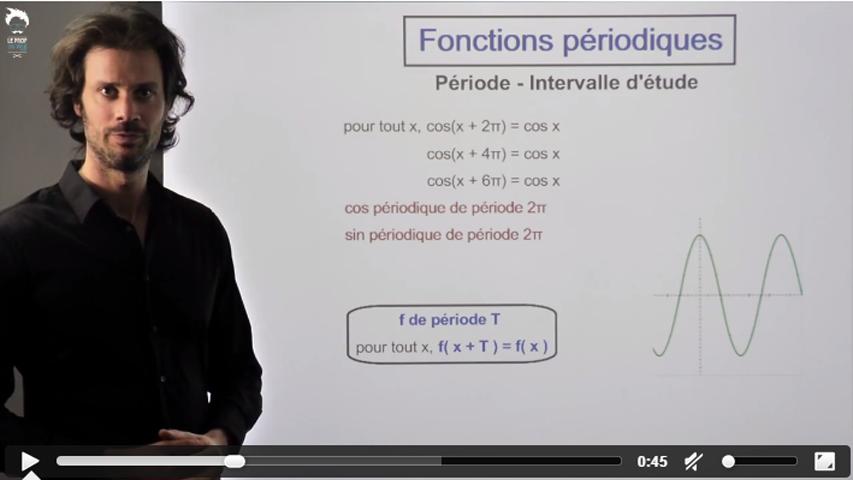
Dans cette vidéo, tu vas apprendre à étudier une fonction périodique à travers un exemple.
Au programme :
- détermination de la période
- choix de l’intervalle d’étude
- calcul de la dérivée
- étude de son signe via une inéquation trigo
- tableau de variation
- tracé.
Toutes les questions les plus courantes sur les fonctions contenant des cos ou sin.
5 min 41 s
Un problème de synthèse qui reprend les questions classiques du chapitre en les intégrant dans un contexte économique. Un entrainement à faire absolument avant un DS! On y voit au passage les fonctions d'offre et de demande, la notion de prix d'équilibre et comment relier recette, coût et bénéfices. des incontournables des maths en filière éco ! La vidéo pour faire la différence.
4 min 54 s
C'est l'objectif de base de cette partie du chapitre.
Trouver une équation de droite à partir d'un point et d'un vecteur directeur et inversement.
On voit dans cette vidéo comment résoudre ce problème uniquement avec des connaissances de seconde en passant par la pente.
L'avantage de cette méthode intuitive, c'est qu'elle reprend des notions que tu connais déjà et que tu réutiliseras souvent. Un bon moyen de renforcer sa maitrise sur les droites et les vecteurs !
L'inconvénient : il y a plus rapide.
Si tu as besoin de rappels sur les bases de Seconde, regarde ces vidéos sur la pente et les équations cartésiennes.
9 min 16 s
Une suite définie par récurrence est étudiée par l’intermédiaire de la fonction associée.
Pas facile de comprendre ce que ça veut dire à la première lecture…
Mais interdiction de partir en courant car la moitié des problèmes de suite sont de ce type, alors prends le temps de regarder cette vidéo pour savoir ce qui t’attend en DS ou au Bac.
- toutes les clefs pour réussir ces classiques du Bac
- en prime quelques astuces.
Une vidéo qui peut te faire gagner à elle toute seule quatre ou cinq points !
Remarques : si tu ne comprends pas pourquoi on doit justifier que la fonction est croissante dans les hérédités, regarde cette vidéo.
Et si tu as des difficultés à retourner la relation entre Un et Vn, tu peux t’entrainer avec cette vidéo.
6 min 13 s
L’enquête sur la disparition de Monsieur X se poursuit…
Vous venez de découvrir chez Monsieur X des relevés de radar de police !?
Vous cherchez à comprendre pourquoi certaines fréquences ont été nerveusement entourées.
Un exercice très complet pour s’entraîner à calculer une vitesse grâce à l’effet doppler, et en particulier pour étudier, à fond et en détails, le fonctionnement d’un radar.
Si tu as des difficultés à manipuler des formules de physique avec plusieurs lettres, regarde d’urgence cette vidéo.
4 min 39 s
On cherche à découvrir un moyen de lire le code d’un coffre réputé inviolable.
Un exercice très complet sur la diffraction.
Si tu as des difficultés à manipuler des formules de physique avec plusieurs lettres, regarde d’urgence cette vidéo
3 min 34 s
Une série d’exercices assez coriaces qui demandent de maitriser la trigo et les intégrales.
Quatre intégrales à calculer.
Difficulté croissante…
4 min 28 s
Cette fois on doit construire le tableau de variations de fonctions quotients. Un grand classique des DS sur la dérivation. Attention à l'ensemble de définition !
2 min 28 s
Je te montre comment déterminer la période d'une fonction contenant un cos ou un sin.
On voit aussi pour les fonctions cos(nx) ou sin(nx), l'effet du n sur la période.
des bases importantes pour comprendre et étudier des fonctions périodiques.
4 min 47 s
On voit comment tracer les fonctions cos(x) et sin(x).
Ce qui est spécial avec ces fonctions périodiques,
c’est qu’on s’intéresse à leur période et à leur parité pour réduire leur intervalle d’étude.
Une approche toute nouvelle pour toi.
des fondamentaux indispensables pour étudier toutes les fonctions périodiques contenant des cos et sin.
5 min 10 s
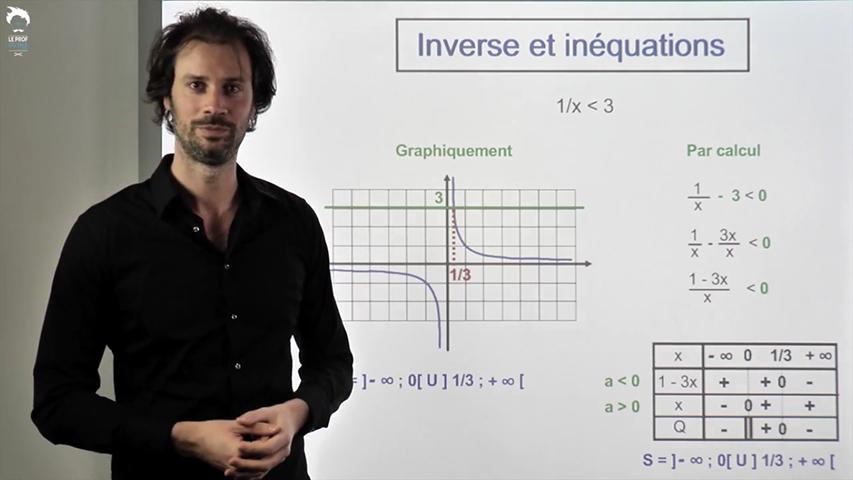
L'exercice le plus important du chapitre !
D’abord parce que c'est celui qui tombe le plus souvent en DS sur la fonction inverse.
Tu le sais maintenant…
Mais aussi parce qu'on y voit une méthode qui vous servira tout le reste du lycée : étudier le signe d’un quotient avec un tableau de signes.
Une technique indispensable pour la suite ! A voir et revoir !
Avant de visionner cette vidéo, n’hésite pas à te remettre dans le bain sur deux savoir faire indispensables ici : comment trouver le tableau de signes d'une droite et comment résoudre graphiquement une inéquation.
7 min 15 s
Une vidéo qui va t'aider à maîtriser et mémoriser la liste des formules
- d'addition
- de soustraction,
- de duplication,
- de linéarisation.
des fonctions cos et sin.
Un vrai plus si tu veux te donner toutes tes chances de retenir ces formules.
1 min 55 s
Une inéquation de bon niveau.
Un type d'inéquation qu'il faut savoir résoudre pour les études des fonctions trigo de Terminale.
5 min 53 s
Savoir calculer des fonctions dérivées, c'est la base pour réussir les exercices et problèmes de ce chapitre.
Une série d'exemples pour maitriser cette étape incontournable, éviter les erreurs et gagner du temps.
Une vidéo à voir absolument.
5 min 22 s
deux formules pour gagner du temps d'abord, puis une série de formules qui te permettront de dériver n'importe quelle fonction !
Je te montre une technique très pratique pour toutes les mémoriser d'un coup !
Une méthode qui vaut le détour…
Attention ! Les formules de cette seconde partie de la vidéo sont à la limite du programme.
Elles ne sont pas toujours présentées en Première.
4 min 55 s
Points d'intersection et position relative.
Dans de nombreux problèmes il y a deux fonctions.
Comment faire pour obtenir leur intersection à partir de leur formule ?
Et qu'est ce que signifie "étudier la position relative de deux courbes"?
deux questions que tu vas retrouver régulièrement pendant toutes tes années de lycée.
5 min 22 s
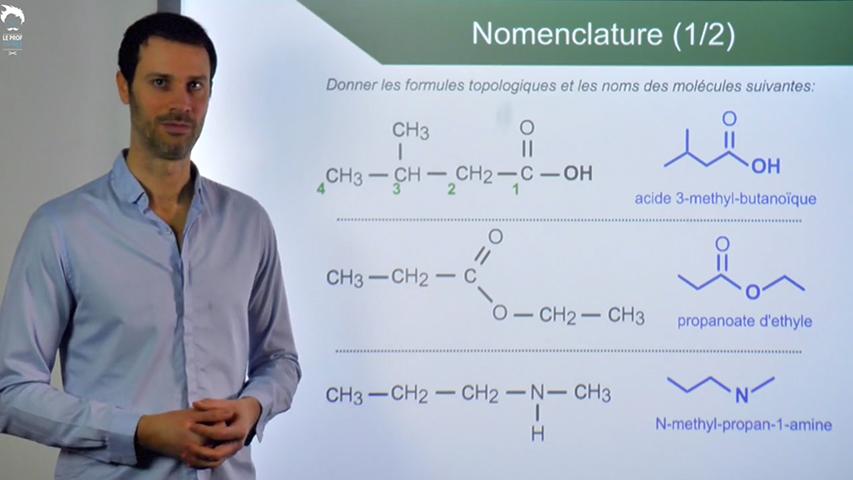
Vous avez une formule de la molécule. Il faut la nommer. Il est indispensable de maîtriser les groupes caractéristiques et les fonctions au programme de Terminale. On s’entraîne aussi à passer d’une formule développée à la formule topologique associée, et inversement, qui sont d’autres questions classiques de chimie organique.
6 min 57 s
Quelle est la molécule à l’origine de l’ivresse ? Quels sont sa formule chimique et son groupe caractéristique ? Surtout, on voit comment est prise en compte la présence d’un groupe caractéristique quand on doit nommer une molécule. Enfin on présente les groupes caractéristiques et fonctions à connaître au bac. Tout simplement incontournable.
2 min 49 s
Un bilan pour faire le point sur tout ce qu'il faut savoir sur les fonctions homographiques.
1 min 57 s
Après certaines lésions, le système nerveux central est capable de récupérer ses fonctions. Voyons cela dans le cas das zones motrices.
3 min 15 s
Retour à la forge. Cette fois notre chevalier tente de refroidir une énorme hache dans un seau d’eau. On cherche la quantité d’eau qui restera dans le seau à la fin de l’opération. Une autre occasion d’utiliser les concepts de capacité thermique massique et de chaleur latente de changement d’état. Si tu as des difficultés à isoler une variable ou retourner des formules, je te conseille de regarder href="https://www.leprofduweb.com/terminale/s/mathematiques/etude_de_fonctions_:_methode_et_astuces_pour_reussir/isoler-une-variable-cours-video-bac" de méthode.
3 min 18 s
On fait fondre des glaçons dans un thermos contenant 2 L d’eau et on cherche la température finale du mélange. Un classique. Si tu as des difficultés à isoler une variable ou retourner des formules, je te conseille de regarder href="https://www.leprofduweb.com/terminale/s/mathematiques/etude_de_fonctions_:_methode_et_astuces_pour_reussir/isoler-une-variable-cours-video-bac" de méthode.
3 min 43 s
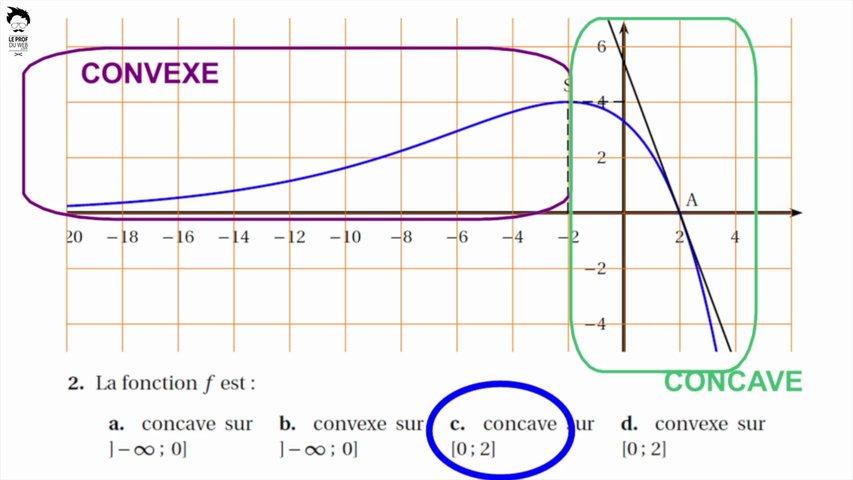
On a la courbe d’une fonction.
Tout se fait par lecture graphique.
Dans la vidéo précédente , on a vu des méthodes qui te permettront normalement de répondre à 2 des 4 questions.
En cas de difficulté sur la question de convexité regarde cette vidéo
et si n’a pas réussi à estimer l’intégrale tu peux t’entrainer ici.
2 min 26 s
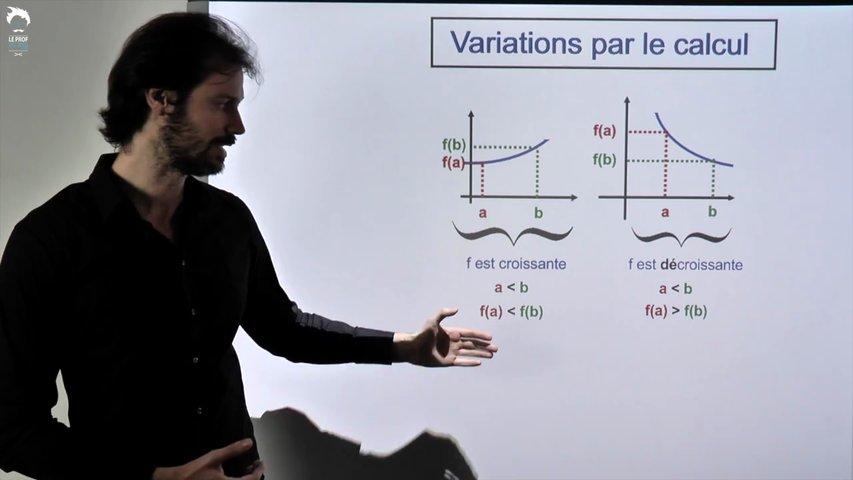
On voit ici une méthode pour trouver les variations d’une fonction sans sa courbe.
Elle porte une idée qui vous aidera à comprendre de nombreux cours de Première et Terminale.
Pour l'instant, elle sert surtout aux démos (variations des fonctions inverse et carré)
Parfois pour étudier les variations d'une fonction que vous ne savez pas tracer, un exercice un peu abstrait présenté dans la vidéo suivante.
2 min 29 s
On voit comment changer l'écriture d'une fonction homographique.
Le but: trouver une forme qui permet de trouver les variations.
Un classique de première avec des conseils de méthode qui vous aideront jusqu'au bac!
7 min 8 s
Pour s’entrainer, un problème de synthèse, type DS, intégralement corrigé en vidéo, comme toujours.
A la question 5, une erreur de copie s'est glissée dans le corrigé.
Nous avons résolu l'inéquation (3x+10) / (x+2) < -2 au lieu de (3x-10) / (x+2) < -2...
Si l'on résout la seconde inéquation on doit trouver ]-2 ; 6/5[ en suivant la même méthode et les mêmes étapes que dans le corrigé en vidéo.
2 min 28 s
On s'entraîne à construire l'allure et le tableau de variation de plusieurs fonctions homographiques.
On voit aussi comment trouver leur centre de symétrie.
3 min 40 s
Une série d'exercices où il faut trouver l'ensemble de définition de fonctions comportant des racines ou des quotients. Une base pour de nombreux exercices de fin Première ou Terminale.
5 min 5 s
Tout simplement l'exercice le plus important du chapitre.
Il peut prendre deux formes:
1) on vous demande le tableau de signes d'une fonction homographique
2) vous devez résoudre une inéquation qui vous ramène à… un tableau de signes !
Bref, vous aurez compris, vous avez intérêt à bien maitriser les tableaux de signes de quotients.
Pour se préparer à cet exercice un peu technique, au besoin, remets-toi au clair sur
- Comment mettre au même dénominateur ?
- Le tableau de signe d'une fonction affine.
- La fonction inverse et inéquations.
7 min 35 s
Cette fois, on s’attaque à un grand classique de début d’année de Terminale :
l’étude d’une fraction rationnelle dont il faut changer l’écriture pour trouver ses limites.
La méthode utilisée est une identification.
Si cela ne te parle pas, c’est une très bonne raison de regarder cette vidéo car l’identification,
méthode croisée en Première, est considérée comme connue par beaucoup de professeurs…
Une vidéo à voir absolument sur une méthode que tu dois maitriser pour le Bac.
Si tu veux continuer à t’entrainer sur cette méthode,
tu peux travailler avec cette vidéo sur les polynômes
ou avec celle-ci sur les fonctions homographiques
3 min 38 s
Ensemble de définitions, images, antécédents, c’est sur ces notions qu’on vous interroge le plus souvent au début d’un problème sur les fonctions homographiques.
des questions plutôt simples et donc des points à ne surtout pas laisser !
5 min 59 s
Cette fois, on affronte le problème inverse, un autre incontournable des exercices de chimie organique : à partir de son nom donner les formules semi-développée et topologique d’une molécule. C’est l’occasion d’une bonne révision des groupes caractéristiques et de leurs fonctions associées.
2 min 22 s
On trace l’allure de la fonction cube. On en déduit son tableau de signes et son tableau de variations qu’il faut retenir. Enfin, on explique la nécessité d’une nouvelle méthode pour étudier les variations de fonctions comportant des racines ou des cubes et d’autres fonctions. Cette nouvelle technique, c’est la dérivation, sujet du chapitre suivant.
2 min 37 s
La démonstration par le calcul des variations de la fonction inverse.
Pour assurer une interro de leçon si tu as un professeur qui vous demande de refaire les démos ou pour découvrir des mathématiques plus abstraites si tu te sens à l'aise sur le reste.
En cas de difficultés, cette vidéo cette vidéo devrait t’aider.
8 min 39 s
Si on veut la dérivée d'une fonction en différents points, il est inutile de recalculer à chaque fois le taux d'accroissement.
Pourquoi ? Parce qu'on peut calculer une fois pour toute une formule !
Mieux on va mémoriser cette formule pour ne plus avoir à la recalculer !
Bref, à partir de maintenant on ne calculera plus des dérivées en un point mais des fonctions dérivées.
On démontre ici les formules des fonctions dérivées des fonctions « carré », « inverse » et « racine ».
Trois démos souvent à restituer en devoir.
8 min 39 s
Les formules de dérivation sont à connaître sur le bout des doigts. Elles sont un peu les tables de multiplication de la Terminale.
On voit ici comment les retrouver, les mémoriser et les utiliser efficacement.
Une vidéo à voir et revoir !
Si tu ne te sens pas à l'aise avec les puissances, regarde cette vidéo : mise au point sur les puissances.
4 min 35 s
Les puissances négatives de type « un sur x puissance n » ou plus généralement les quotients avec une puissance au dénominateur sont rarement l’objet d’étude de fonctions.
On peut néanmoins vous demander de les dériver pour une interro de leçon sur la dérivée ou dans un QCM.
On y voit deux méthodes.
La deuxième, la plus rapide, vous sera aussi indispensable dans le chapitre sur les Primitives.
3 min 27 s
On démontre par le calcul c'est-à-dire sans s'appuyer sur l'allure de la fonction carré pourquoi elle est croissante sur les positifs et décroissante sur les négatifs.
Une méthode pour étudier les variations qui resservira aux Premières S.
En cas de difficultés, cette vidéo devrait t’aider.
5 min 30 s
Il est assez facile d’imaginer ce qui se passe si on tire avec une mitraillette à travers une ouverture percée dans un blindage.
Mais que se passe-t-il si on fait la même chose avec un rayon de lumière ?
On va voir qu’apparait une figure étrange constituée d’une tâche centrale et d’anneaux alternativement sombres et clairs.
C’est ce qu’on appelle une figure de diffraction.
On se concentre dans cette vidéo sur les conditions d’apparitions de ce phénomène et les dimensions de sa tâche centrale.
Dans la vidéo suivante, on expliquera l’origine de l’alternance des anneaux sombres et clairs dont l’origine provient d’un phénomène appelé interférences.
Si tu veux comprendre pourquoi pour un angle petit, on peut affirmer que cet angle a une valeur en radian très proche de son sinus et de sa tangente, regarde cette vidéo.
Et si tu as des difficultés à manipuler des formules de physique avec plusieurs lettres, regarde d’urgence cette vidéo.
3 min 34 s
Dans le chapitre des suites, on a appris à ajouter, soustraire, multiplier et diviser des limites.
Tout ça reste valable pour les fonctions.
La seule nouvelle opération, c’est la composition de limites.
On voit comment trouver quelques limites où l'une des opérations est une composition de fonctions.
Si tu as des difficultés à reconnaitre des composées, regarde cette vidéo en deux minutes, tes doutes seront envolés.
3 min 4 s
Qu'est ce qu'une fonction homographique ?
Comment faire pour décider si une fonction est ou non homographique ?
Du cours mais aussi un exercice classique des DS…
2 min 35 s
Une vidéo pour éviter une erreur fatale !
Comme vous n’avez pas appris la composition en Première,
beaucoup d’entre vous ne reconnaissent pas les composées
et les prennent pour des produits.
La dérivée est alors fausse et avec elle tout le début de l’étude de fonction…
Un petit problème de vision qui coûte très cher.
2 min pour apprendre à reconnaitre la forme globale d’une dérivée et ne plus faire cette erreur…
7 min 54 s
Les limites de référence, ce sont les seules limites que tu peux donner sans justification.
Ce sont les limites de cours, théoriquement à apprendre.
En réalité, elles peuvent se retrouver très facilement.
Je te présente deux techniques pour retrouver les limites des fonctions de référence :
- par le graphique
- par le calcul.
4 min 37 s
On se concentre maintenant sur l’application la plus courante de l’effet doppler comme moyen de mesurer une vitesse.
On expose d’abord le cas le plus simple puis on se penche sur le fonctionnement un peu plus subtil d’un radar de police.
Une vidéo incontournable ! Et d’autant plus qu’on y présente le bilan de l’essentiel sur l’effet doppler…
Si tu as des difficultés à manipuler des formules de physique avec plusieurs lettres, regarde d’urgence cette vidéo
7 min 55 s
Vous avez réussi à violé le code du coffre présenté dans le problème précédent. Bien joué !
Malheureusement, maintenant, vous avez la police à vos trousses …
Vous entendez le son de leur sirène plus aigu puis plus grave…
Est-ce bon ou mauvais signe et pourquoi ?
L’effet doppler permet de répondre à cette question et à bien d’autres encore que l’on présente dans cette vidéo dont les phénomènes de « blueshift » et « redshift ».
Si tu as des difficultés à manipuler des formules de physique avec plusieurs lettres, regarde d’urgence cette vidéo.
3 min 0 s
Qu'on te donne un graphique ou une formule tu dois pouvoir reconnaitre au premier coup d’œil les fonctions affines et linéaires.
En général c'est facile, mais il existe quelques cas moins évidents.
4 min 24 s
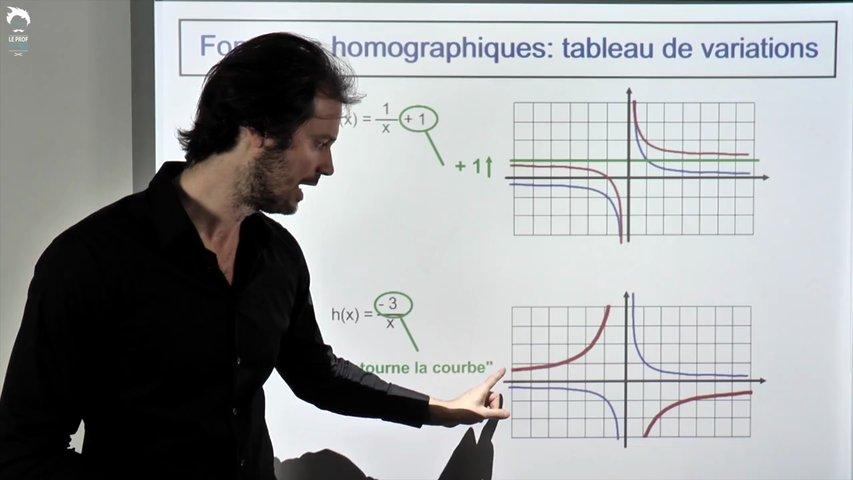
On voit et on explique étape par étape comment construire l'allure et le tableau de variations d'une fonction homographique.
5 min 6 s
S'il y a des quotients avec des x en haut et en bas... vous n'avez plus le choix, il faut passer par un tableau de signe. A voir absolument.
8 min 7 s
Dans cette seconde vidéo de méthode sur les études de fonctions, on revoit comment répondre efficacement à plusieurs questions classiques :
- Variations
- Limites
- Tangente
- Position relative de deux courbes
- Tracé
8 min 56 s
Un problème qui regroupe les questions les plus classiques en devoir sur la loi normale.
On y verra notamment comment utiliser la calculatrice quand les valeurs ne tombent pas « pile » sur des valeurs de référence.
Une vidéo incontournable pour réussir les questions qui tombent le plus souvent sur cette loi.
4 min 15 s
des bases qui te serviront tout au long du chapitre
Bonne nouvelle, on a jeté le compas...
3 min 34 s
Une vidéo pour te tester et voir si tu as bien compris comment tracer les graphiques présentés dans la vidéo précédente.
3 min 21 s
Réaliser des Tracés dans un repère orthonormé est un exercice de début de leçon
qui revient très rarement par la suite en Terminale,
mais un savoir-faire très utile dans le supérieur où il sert dans de nombreux domaines.
5 min 3 s
On construit le tableau de variations d'un polynôme de degré 2 puis on calcule les équations de deux de ses tangentes.
On voit enfin comment utiliser les tangentes pour faire un tracé précis de la courbe.
Un exercice classique à maîtriser absolument !
En cas de difficultés je te propose trois vidéos :
Une vidéo pour savoir comment trouver le signe d'une fonction affine.
Une autre pour comprendre la formule qui donne l'équation d'une tangente.
Et une troisième pour réussir ses Tracés de droite.
3 min 48 s
On a déjà vu les limites de Suites. Dans cette vidéo :
- on fait le point sur tout ce que tu peux réutiliser avec les fonctions.
- on présente aussi les nouveautés qui seront détaillées dans les vidéos suivantes.
Une vidéo pour savoir où tu vas avant de te lancer ou pour faire le point à la fin du chapitre.
Elle peut t’aider à préparer ta fiche sur ce chapitre.
13 min 1 s
Un deuxième sujet de bac corrigé d’un niveau nettement supérieur.
Mais c’est tombé au bac… et vous pouvez avoir ce genre de problème en DS alors il faut s’y préparer.
Je l’ai choisi car je sais que vous êtes souvent désorienté
la première fois que vous devez étudier une famille de fonctions.
Alors pour que vous ne soyez pas surpris en devoir ou au bac,
on voit ensemble comment s’y prendre. Tu y trouveras :
- Calcul de dérivées
- Limites
- Tableaux de variations
- Croissances comparées
- Questions d’interprétation graphique
- Calcul d’aires (si tu as vu le chapitre Intégrales et Primitives)
Si tu ne te sens pas à l’aise avec les questions d’interprétation graphique, regarde cette vidéo de méthode et la suivante.
2 min 0 s
Calculer l’équation d’une tangente est une question courante dans les études de fonctions.
La procédure est très simple dès qu’on maîtrise la méthode.
Si tu n’es plus très sûr de savoir tracer une tangente, autrement dit une droite, regarde cette vidéo.
3 min 23 s
Un bilan sur l'essentiel de ce qu'il faut savoir pour étudier une fonction, pour t'aider à voir si tu maitrises tout ou pour repérer vite fait ce que tu ne sais pas encore.
1 min 55 s
Pour commencer et se faire une idée de ce qu'il faut savoir dans cette leçon ou pour vérifier qu'on a tout compris, le bilan du chapitre droites/ fonctions affines.
6 min 55 s
Je te donne ici, sur des exemples, des conseils de méthode pour réussir tes calculs de dérivées.
Une sécurité pour aborder les études de fonctions.
2 min 46 s
Dès que vous aurez vu les vecteurs vous aurez une technique très rapide
pour prouver l'alignement de trois points (qui vous servira tout le reste du lycée).
Mais en attendant il faut savoir prouver l'alignement avec le cours sur les droites...
Un peu long, mais pas très difficile si tu maîtrises ce qu'on a vu dans cette vidéo.
1 min 44 s
Parfois la formule pour calculer la pente à partir des coordonnées de deux points ne marche plus.
Pourquoi ?
Et comment faire ?
Une vidéo pour anticiper des cas particuliers et les gérer en 30 secondes montre en main.
3 min 44 s
Avec les fonctions affines, toutes les questions habituelles (images, antécédents, tableau de variations et de signes) sont très simples à résoudre.
On va donc se poser à leur sujet des questions bien spécifiques que je te présente ici.
En un mot, tout ce qu'il faut savoir faire avec les fonctions affines ou si tu préfères « avec les droites ».
5 min 30 s
deux autres fonctions étudiées avec cette méthode.
L'une comporte une racine et la seconde un quotient
avec des x en haut et en bas...
Cela n'est pas du tout anodin, nous le verrons.
A voir absolument! Grand classique.
3 min 13 s
On applique la troisième loi de Kepler pour étudier les satellites géostationnaires. On explique d’abord ce que sont les satellites géostationnaires, où ils doivent se situer et pourquoi. Enfin, on détermine l’altitude à laquelle ils doivent être envoyés. Un classique là encore, à maîtriser parfaitement. Si tu as des difficultés à retourner les formules en Physique pour isoler une variable je te recommande cette vidéo.
3 min 15 s
L’eau de votre bain commence à se refroidir. Vous y rajoutez un peu d’eau bien chaude. Quelle est la température du mélange ? Un autre grand classique. Tout aussi incontournable que l’exercice précédent. A noter qu’on le résout avec deux méthodes : - intuitivement, en raisonnant sur les quantités de chaleurs échangées. - en passant par l’énergie interne. Si tu as des difficultés à isoler une variable ou retourner des formules, je te conseille de regarder cette vidéo de méthode.
4 min 13 s
Une vidéo de méthode qui passe en revue les techniques à utiliser pour d’autres équations dans C.
Un conseil : note celles qui ne te semble pas évidentes.
Enfin, si tu ne te sens pas à l’aise quand il faut retourner des formules ou isoler une variable,
regarde cette vidéo de méthode.
2 min 18 s
On démontre par calcul la croissance de la fonction carrée.
C'est l'occasion de découvrir la quantité conjuguée, un outil
qui pourra vous servir dans d'autres situations.
Si tu ne comprends pas la méthode d'étude des variations utilisée dans la vidéo,
regarde ce rappel ou cette démo de seconde
3 min 40 s
Une série d'exercices où il faut trouver l'ensemble de définition de fonctions comportant des racines ou des quotients.
Une base pour de nombreux autres exercices de ce chapitre. A maitriser absolument avant un DS.
En cas de difficultés sur les taleaux de signe de polynôme revois ces deux vidéos.
- Racine et tableau de signes 1/2
- Racine et tableau de signes 1/2
3 min 6 s
Les fonctions q puissance x sont des « cousines » de l’exponentielle.
Tu dois en connaître quelques propriétés générales.
Elles sont rarement présentes dans les sujets de bac.
A maitriser principalement avant une interro sur chapitre.
5 min 36 s
Dans une étude de fonction de niveau Bac, il y a souvent deux fonctions liées l’une à l’autre.
Cette vidéo te montre comment bien gérer les passages entre elles dans les deux principaux cas de figure :
- Avec une fonction auxiliaire
- Avec une dérivée seconde
6 min 24 s
Dans cette seconde vidéo de méthode sur les études de fonctions,
on revoit comment répondre efficacement à plusieurs questions classiques :
- Variations
- Tangente
- Position relative de deux courbes
- Tracé
2 min 25 s
Pour étudier le signe d'une expression, tu dois d’abord savoir quelle méthode appliquer.
Dans cette première partie nous expliquons comment choisir la bonne méthode sans perdre de temps.
Remarques: certaines méthodes sont découvertes en cours d'année de Terminale
donc pas de panique si tu ne comprends pas tout en début d'année.
Enfin, si tu veux revoir comment étudier rapidement le signe d’une fonction affine,regarde cette vidéo.
Et pour le signe d’un polynôme cette vidéo et la suivante.
3 min 56 s
Pour intégrer les fonctions de type « 1 sur x puissance n », il vaut mieux connaître la méthode.
Elle te permettra également de trouver les primitives les plus complexes du programme.
Un point méthode pour les cas difficiles.
Important pour une interro spéciale primitive.
Plus improbable pour un devoir bilan ou le bac.
En cas de difficultés, je te conseille de regarder cette vidéo sur la dérivation des puissances négatives.