




Assez simple
01 Qu'est-ce qu'une fonction ?
Qu'est ce qu'une fonction?
A quoi ça sert ?
Connais-tu les trois moyens de les définir?





Assez simple
Qu'est ce qu'une fonction?
A quoi ça sert ?
Connais-tu les trois moyens de les définir?




Très facile
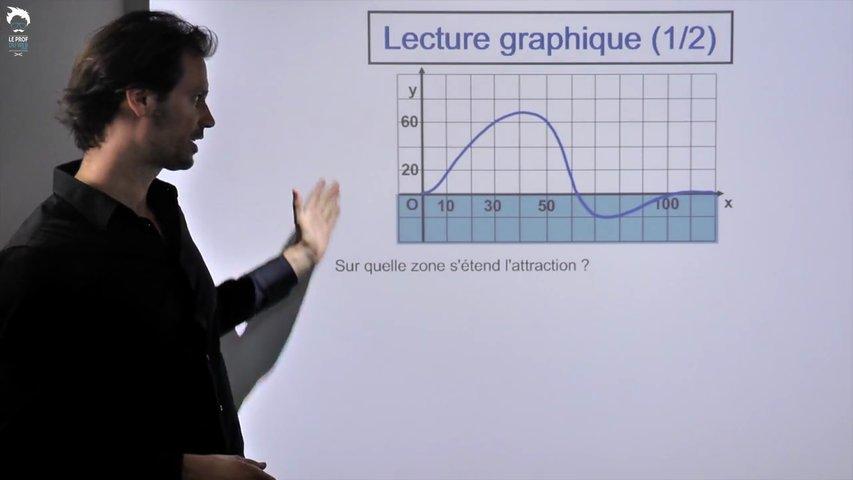
Ensemble de définition, images, antécédents, équation, inéquation.
Comment résoudre graphiquement ces types de questions?




Assez simple
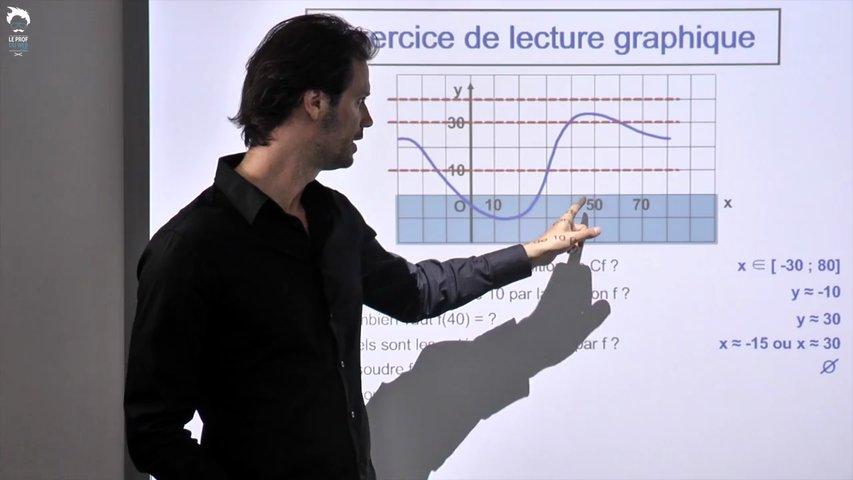
Un exercice d'application pour s'entraîner suivi du problème inverse : construire une courbe compatible avec un tableau de signes et un tableau de variations.




Assez simple
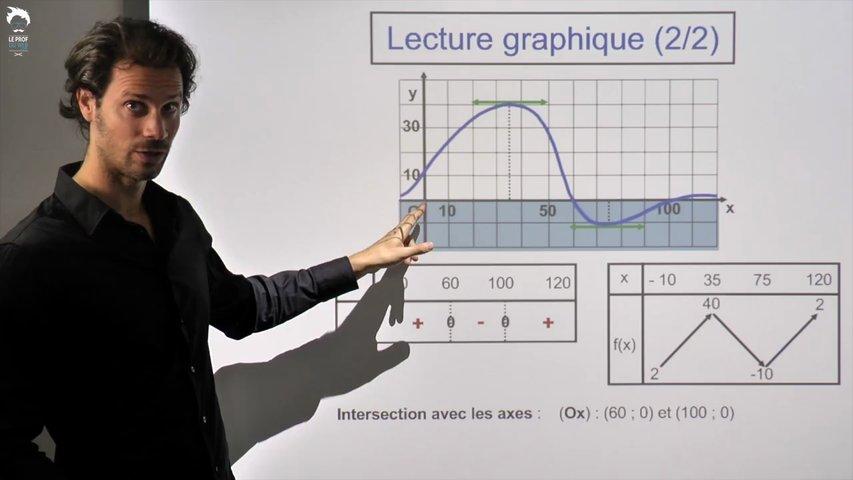
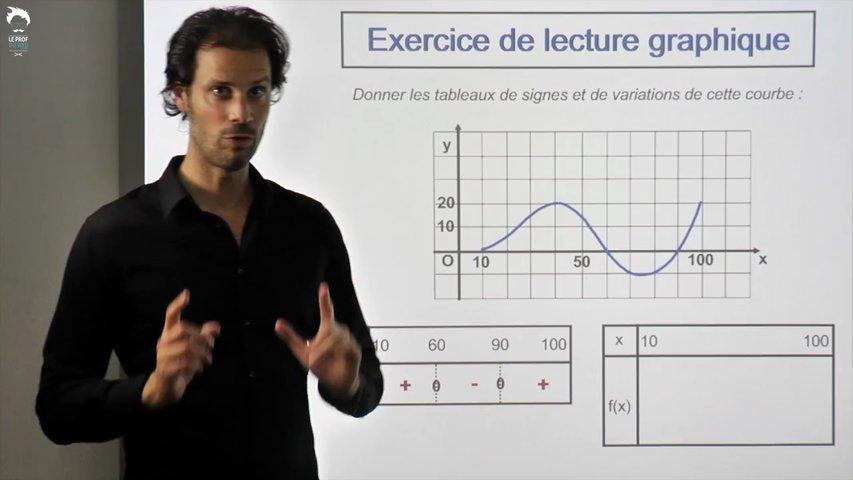
Cette fois, à partir d'une courbe, donc toujours graphiquement, on va voir comment construire le tableau de signes et le tableau de variations d'une fonction.




Assez simple
Un exercice d'application pour te tester sur tout ce qui a été présenté dans la vidéo précédente.
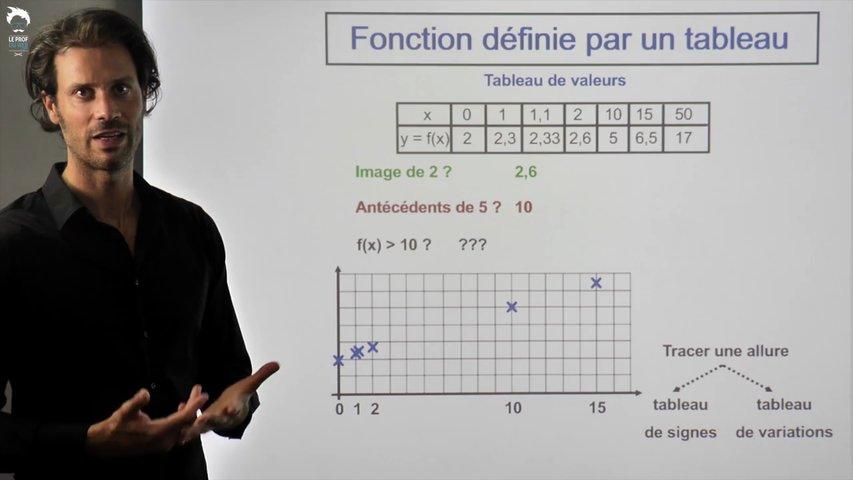




Très facile
Que peut-on faire avec une fonction uniquement définie par un tableau ?





D'un bon niveau
Cette fois la fonction est définie par une formule.
On voit les différentes questions auxquels il faudra savoir répondre en Seconde et pendant tout le lycée :
- ensemble de définition
- images
- antécédents
- équations
- inéquations
- tableaux de signes et de variations
On voit plus précisément comment les traduire pour démarrer dans les exos.
Une vidéo de méthode sur des techniques qui servent à longueur de temps.
Un bilan sur l’essentiel de ce qu'il faut savoir et savoir faire pour étudier une fonction.
Des bases indispensables pour tout le lycée !
Un bon moyen de faire le point sur ce que tu sais.





Assez simple
Un bilan sur l'essentiel de ce qu'il faut savoir pour étudier une fonction, pour t'aider à voir si tu maitrises tout ou pour repérer vite fait ce que tu ne sais pas encore.
Savoir décrire un extremum.
Trouver l'intersection de deux fonctions ou étudier leur position relative.
Des questions que vous rencontrerez tout le lycée quand vous étudiez des fonctions.





D'un bon niveau
Points d'intersection et position relative.
Dans de nombreux problèmes il y a deux fonctions.
Comment faire pour obtenir leur intersection à partir de leur formule ?
Et qu'est ce que signifie "étudier la position relative de deux courbes"?
Deux questions que tu vas retrouver régulièrement pendant toutes tes années de lycée.
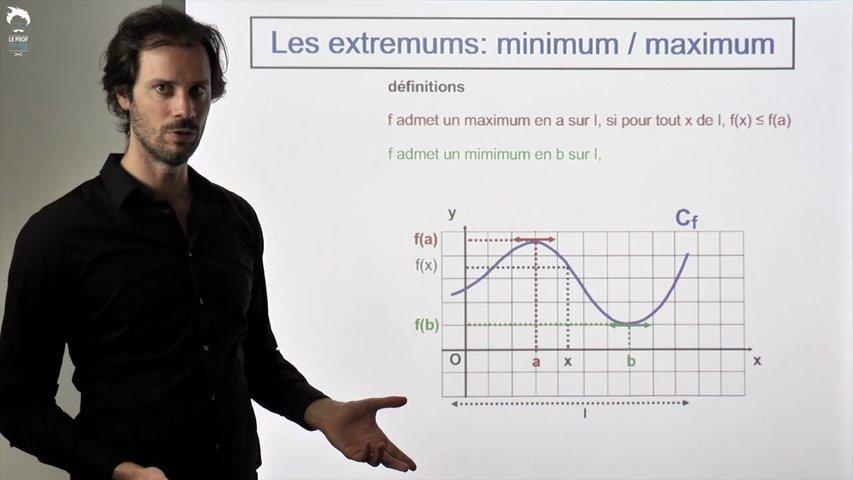




Très facile
Décrire un extremum.
Une question plutôt simple.
Il y a juste une confusion à éviter et une petite phrase de rédaction à apprendre.
Comment faire pour étudier les varations d'une fonction sans son allure graphique ?
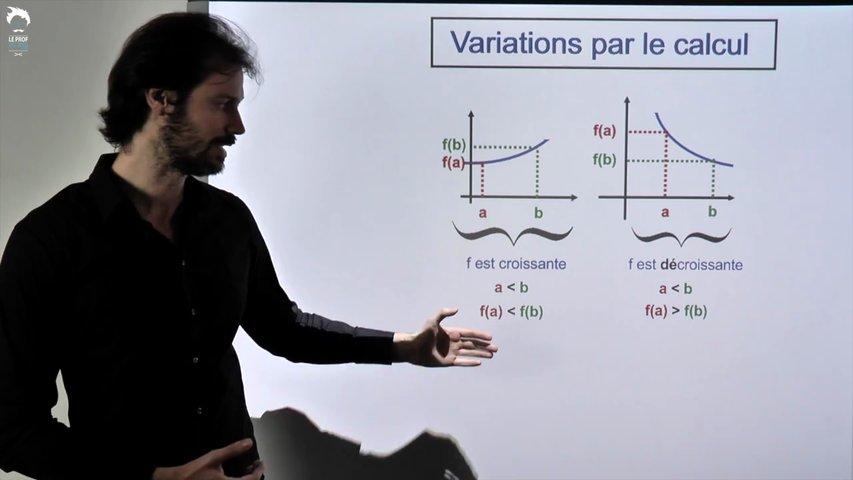




Difficile
On voit ici une méthode pour trouver les variations d’une fonction sans sa courbe.
Elle porte une idée qui vous aidera à comprendre de nombreux cours de Première et Terminale.
Pour l'instant, elle sert surtout aux démos (variations des fonctions inverse et carré)
Parfois pour étudier les variations d'une fonction que vous ne savez pas tracer, un exercice un peu abstrait présenté dans la vidéo suivante.





Difficile
Application de la méthode exposée dans la vidéo précédente.
Un exercice type de niveau fin Seconde dont il est très dur de trouver seul la solution et la bonne rédaction.
Par contre, une fois qu'on a vu deux exemples bien choisis, c'est toujours la même chose…
Deux exemples donc pour t’aider à comprendre comment ça marche.