MA

01  Les Polynômes
Les polynômes de degré 2.
Un chapitre clef du programme de Première qui te servira régulièrement jusqu’au bac.
Ce qu'il faut retenir sur le long terme, c'est comment trouver les racines (valeurs où le polynôme s’annule) et en déduire le tableau de signes.
Mais attention ! Pour réussir un DS sur les polynômes, il te faudra aussi maitriser la recherche du sommet (maximum ou minimum), la construction du tableau de variation et la forme canonique.
Enfin, un conseil: avant de te lancer dans ce chapitre, revois les vidéos de Seconde sur les polynômes
pour partir sur des bases solides.

01
Les bases de la leçon : indispensables pour la suite !

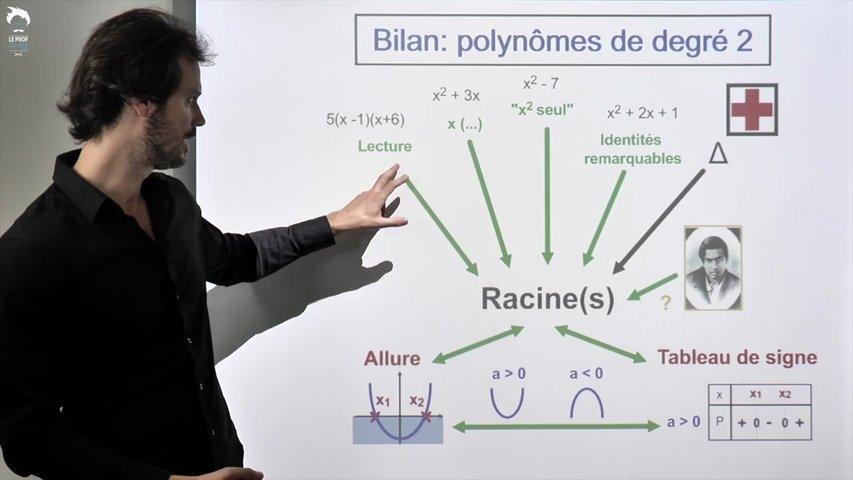
Déterminer les racines puis le tableau de signes ou le sommet puis le tableaux de variations, c’est l’essentiel de ce qu’il faut savoir faire sur les polynômes.
01
Racines et tableau de signes 1/2
5 min 27 s Voir la vidéo

Assez simple

02 Racines et tableau de signes 1/2

On voit ici comment trouver les racines puis le tableau de signes d'un polynôme de degré 2.
Pour l'instant tout peut se faire avec des connaissances de seconde.
Si ça va trop vite, si tu te sens vraiment trop rouillé, prends quelques minutes pour regarder ces vidéos et te remettre dans le bain.
Equations en x² seul
Factorisation avec un facteur commun
Factorisation avec les identités remarquables
Utiliser la forme canonique
Tu y trouveras l’essentiel pour bien suivre la suite ;)

Racines et tableau de signes 2/2
5 min 49 s Voir la vidéo

Assez simple

03 Racines et tableau de signes 2/2

Le delta. On fait appel à lui quand la ou les racines ne peuvent pas se trouver pas simplement.
Mais le delta, qu'est ce que c'est ?
Et comment l'utiliser ?
On voit aussi, à nouveau, qu'avec les racines d'un polynôme de degré 2 on peut très facilement construire son tableau de signes.

02
Deuxième partie du cours : zoom sur les changements d’écriture

Quand on a la forme factorisée ou la forme canonique, c’est très facile d’obtenir la forme développée.
Il suffit de… développer.
Mais en sens inverse, c’est moins évident.
Point méthode pour obtenir rapidement une forme factorisée ou canonique. 
01
La technique de l'indien
4 min 42 s Voir la vidéo

Assez simple

03 La technique de l'indien

Une méthode pour mettre directement un polynôme sous forme factorisée ou, sa première utilité, pour obtenir les racines en évitant le delta…
Un gros raccourci qui fonctionne quand les racines tombent « justes ».
Nous l'appellerons la "technique de l'indien."
Une technique qui a de plus en plus d'adeptes...

Mettre un polynôme sous forme canonique
5 min 37 s Voir la vidéo

Assez simple

04 Mettre un polynôme sous forme canonique

Cette fois, on ne connait pas le sommet.
On va partir de la formé développée et sans passer par le sommet trouver la forme canonique.
Un exercice un peu technique, indispensable pour comprendre la démo du chapitre et un peu plus tard dans l’année, pour transformer des équations de cercle.

03
Démonstrations et bilan

D'où vient b² - 4ac , la formule du delta ?
Comment expliquer les formules des racines ?
Et pourquoi l'abscisse du sommet vaut toujours -b/2a ?
C'est ce que nous allons voir dans la démonstration exposée et expliquée en détails dans cette vidéo.
Avant de la regarder, assure-toi de maîtriser la mise sous forme canonique présentée dans la vidéo précédente et au besoin celle sur les équations avec forme canonique. 
01
Bilan: polynômes de degré 2
2 min 43 s Voir la vidéo

Assez simple

01 Bilan: polynômes de degré 2

Le bilan sur l'essentiel de ce qu'il faut savoir et savoir faire avec un polynôme de degré 2 en première.
Comment trouver les racines puis le tableau de signes ou encore le sommet puis le tableau de variations ?
On revoit les fondamentaux pour tout mettre au clair en trois minutes avant de se lancer dans des exercices d’applications plus complexes.

04
Exercices et problèmes

Ceux qui tombent le plus souvent en DS... Exercices type QCM ou problèmes: les classiques du chapitre qu'il faut maitriser absolument avant un DS.
01
Polynôme mystère
3 min 26 s Voir la vidéo

Assez simple

03 Polynôme mystère

On vous donne une parabole et vous devez trouver la formule du polynôme correspondant. C'est plutôt facile à condition de connaître la méthode. Si tu ne vois pas de quoi je parle, tu sais ce qu'il te reste à faire...

Exercices menant à des équations de degré 2
5 min 41 s Voir la vidéo

Assez simple

04 Exercices menant à des équations de degré 2

Résoudre une équation de degré 2, c'est-à-dire trouver les racines, maintenant tu sais le faire.
Malheureusement, dans les contrôles il y a parfois quelques étapes de démarrage ou de traduction pas toujours évidents à gérer.
C'est là dessus que s'attarde cette vidéo.
Comment bien partir dans les exercices pour retomber sur les bases de cette leçon.
A voir pour anticiper les difficultés.
Si tu ne connais pas la technique de l’indien, elle est présentée un peu plus haut dans ce chapitre (partie 2).

05
Problèmes plus difficiles

Des problèmes et exercices types un peu plus difficiles donnés parfois en DM, parfois en DS.
A ne pas manquer avant un DS bilan sur le chapitre,  si vous ne voulez pas tenter le diable!
01
Équations de degré 3
3 min 34 s Voir la vidéo

Assez simple

01 Équations de degré 3

Équation de degré 3. Et oui ! Dans le chapitre des polynômes de degré 2, on peut rencontrer des équations de degré 3.
Parfois ce sont de "faux problèmes" car elles se ramènent très facilement à des équations de degré 2. Mais ce n'est pas toujours le cas...
Bien sûr, on voit comment traiter les équations simples en "deux temps trois mouvements" et la méthode pour les situations plus délicates. Si tu ne connais pas la technique de l’indien!, il est encore temps ;)

Équation de degré 4
2 min 41 s Voir la vidéo

Assez simple

02 Équation de degré 4

Équations de degré 4. Plus courantes encore que les équations de degrés 3 dans les DS sur ce chapitre.
Celles que vous pouvez résoudre seules sont en général des équations dites bicarrées qui contiennent uniquement des x puissance 4 et des x².
La clef est alors un changement de variable.
Un grand classique à maitriser absolument avant un DS.

Polynôme défini par trois points
4 min 44 s Voir la vidéo

Assez simple

03 Polynôme défini par trois points

On vous dit qu'un polynôme passe par trois points et vous devez retrouver sa formule.
Un bon casse-tête si on n'a pas vu la méthode…
On voit aussi deux variantes qu’on peut croiser en DS :
- Comment faire si on vous donne seulement deux points dont l'un est le sommet ?
- Comment gagner du temps si parmi les trois points, deux sont des racines ?
Incontournable avant un DS !

Polynôme avec paramètre
4 min 16 s Voir la vidéo

Assez simple

04 Polynôme avec paramètre

Un grand classique souvent croisé d'abord en DM.
Vous étudiez une famille de polynôme dont au moins un coefficient varie en fonction d'un paramètre m.
Un exemple pour comprendre : P(x) = x² + mx + (3 +m).
L'objectif est de discuter du nombre de racines en fonction de m.
De loin, l'exercice le plus coriace coriace du chapitre.
Accrochez-vous et ne vous perdez pas dans les deltas…