TU BLOQUES?
Regarde la vidéo du cours pour comprendre
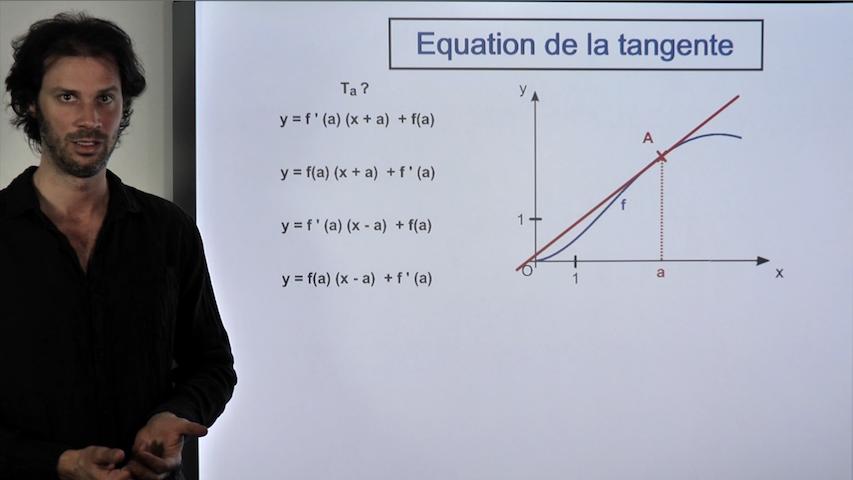
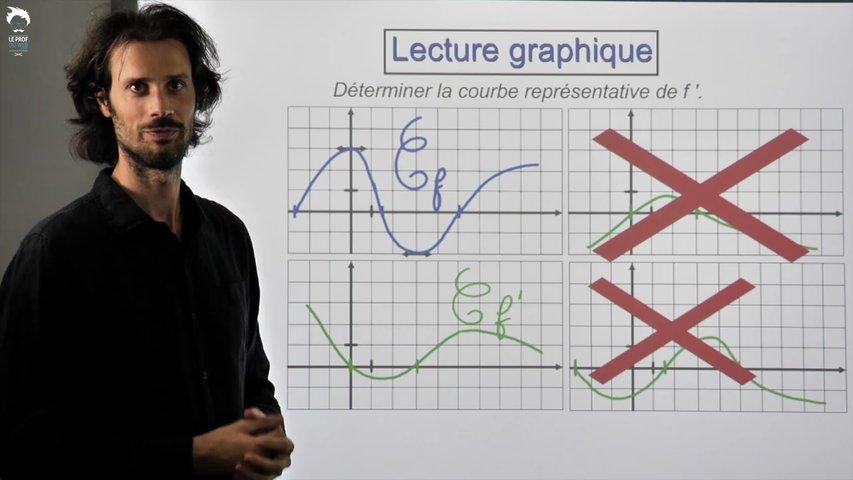
Tableau de variations de fonctions quotients






4 min 28 s
Voir la vidéo




D'un bon niveau