Une première partie où l'on explique concrètement ce qu'est la dérivation avant de construire les premières formules de la leçon.
On commence par une vidéo incontournable pour comprendre vraiment à quoi sert la dérivation.
Ensuite, on enchaîne sur deux vidéos qui se concentrent sur les formules de cours.
Enfin, on s'entraîne à utiliser toutes ces formules:
- on calcule des "nombres dérivées" ou "dérivées en un point" en passant par la formule du "taux d'accroissement".
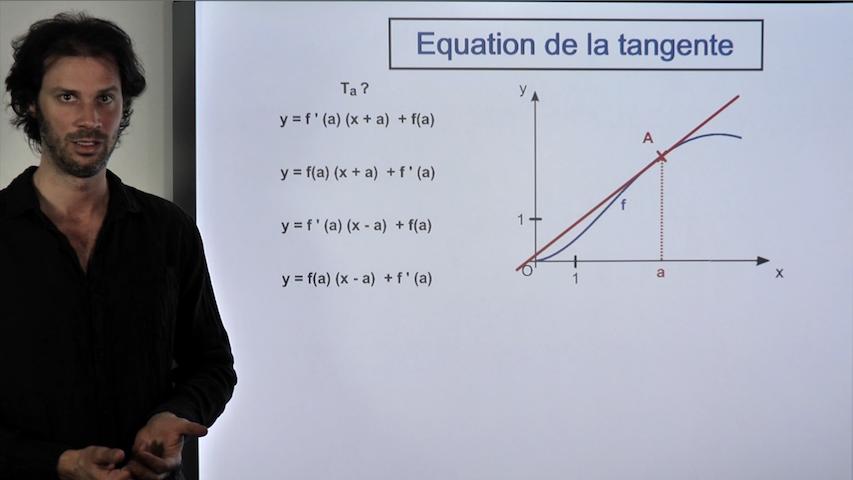
- on utilise les résultats trouvés pour calculer des équations de tangente.
On vient de voir que calculer la dérivée avec le taux d'accroissement est long et lourd.
On apprend ici à calculer des dérivées avec une nouvelle méthode basée sur les formules de dérivation.
On utilise une dernière fois le taux d'accroissement pour démontrer ces nouvelles formules (dans la première vidéo) puis on découvre une liste de formules à apprendre par coeur.
Je te donne comme d'habitude des astuces pour les mémoriser et on apprend à les utiliser efficacement.
Le but principal de la dérivation, c’est la construction de tableaux de variations.
Je te propose de revoir les tableaux de variations les plus classiques de Première.
A maîtriser au plus tôt en Terminale.
Une synthèse de l'essentiel du chapitre pour mettre tes idées au clair avant d'attaquer les problèmes.
On revoit les formules à connaître, quand et comment les utiliser ainsi que les pièges à éviter.
Deux problèmes d'optimisation pour commencer : l'optimisation est un exercice type incontournable que tu auras forcément en devoir...
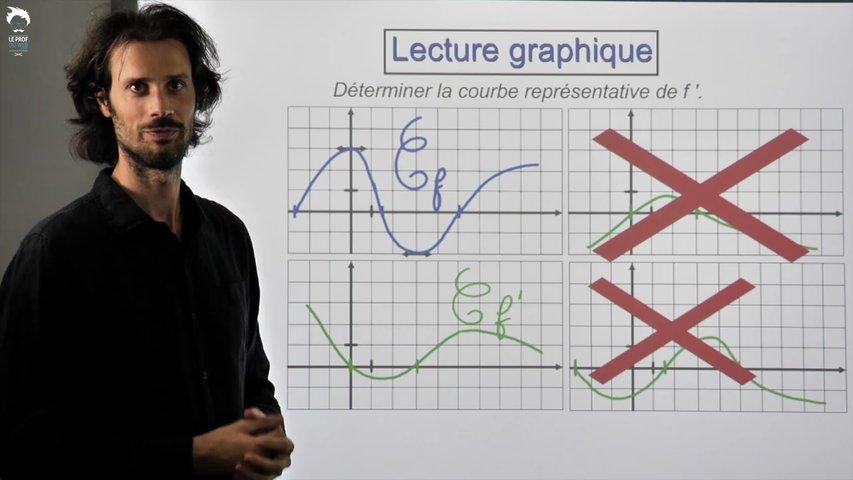
Deux exercices d'interprétation graphique ensuite qui surprennent beaucoup d'élèves.
Ne manque surtout pas cette vidéo pour que ce ne soit pas ton cas.
Enfin, un problème avec des tangentes où les questions sont de moins en moins évidentes...
Un bon moyen de peaufiner ta maitrise de ce chapitre une fois que tu as des bases solides.
Une série exercices que tu devras affronter en DS et que tu recroiseras aussi en Terminale et probablement au bac...
Autrement dit, des exercices types qui méritent que tu y passes du temps.