07  Vecteurs et droites

Très peu de nouveautés dans ce chapitre qui peut être découpé en deux parties.

Tout d'abord des problèmes uniquement sur les vecteurs. Ils sont très proches de ceux rencontrés en Seconde donc n'hésitez pas à revoir le chapitre "Vecteurs" de l'an passé.

En théorie, la grande nouveauté c'est la méthode qui permet de tester la colinéarité de deux vecteurs.
A partir de leurs coordonnées sans passer par un coefficient de proportionnalité qui s'écrit : x y' - x' y = 0.
Mais en pratique, la plupart d'entre vous avez déjà utilisé cette méthode en Seconde. Les différences avec les exercices de Seconde sont donc ailleurs.
Tout d'abord, en Première on vous demande de prendre des initiatives. Pour montrer que deux vecteurs sont colinéaires vous pouvez opter :
- soit pour une décomposition
- soit introduire un repère.
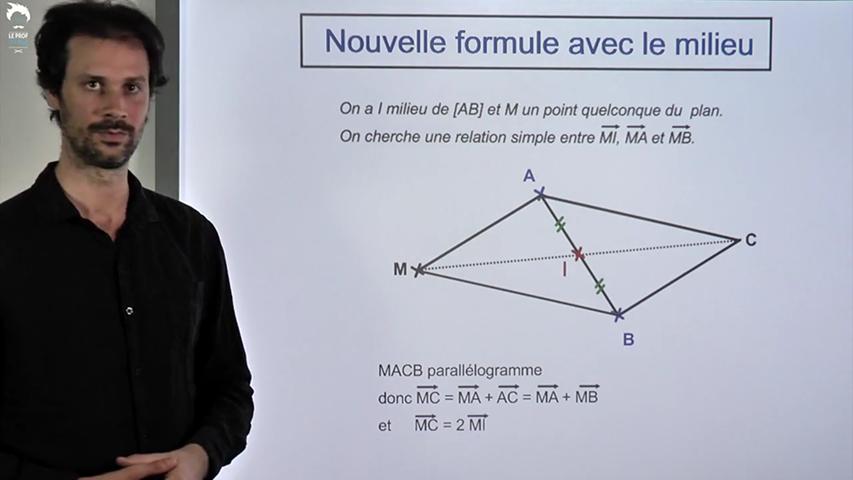
Vous croiserez aussi beaucoup plus souvent des repères quelconques, d'où l'importance de savoir y trouver les coordonnées d'un point. Enfin, vous apprendrez une nouvelle formule reliant milieu et vecteurs.

Dans les problèmes alliant droites et vecteurs, une seule nouveauté: trouver l'équation cartésienne d'une droite à partir d'un point et d'un vecteur directeur et inversement.
Là encore, avec une bonne maitrise des chapitres de Seconde sur les droites tout sera beaucoup plus facile. Cela vaut vraiment la peine de prendre quelques minutes pour se remettre les idées au clair sur les chapitres Fonctions affines et droites et Système et droite.

On commence par rappeler la formule de seconde qui permet de tester si deux vecteurs sont ou non colinéaires puis on la démontre.
En cas de difficultés avec la démonstration, cette vidéo pourrait t'aider.

On démontre d'abord comment trouver une équation cartésienne à partir d'une droite définie par un point et un vecteur directeur.
En observant le résultat, on découvre une passerelle instantanée entre les deux.
Avantage de cette méthode mécanique: elle est ultra-rapide.
Inconvénient: Sortie de ce chapitre, elle ne vous servira plus.
La démonstration repose sur la formule rappelée dans cette vidéo

C'est l'objectif de base de cette partie du chapitre.
Trouver une équation de droite à partir d'un point et d'un vecteur directeur et inversement.
On voit dans cette vidéo comment résoudre ce problème uniquement avec des connaissances de seconde en passant par la pente.
L'avantage de cette méthode intuitive, c'est qu'elle reprend des notions que tu connais déjà et que tu réutiliseras souvent. Un bon moyen de renforcer sa maitrise sur les droites et les vecteurs !
L'inconvénient : il y a plus rapide.
Si tu as besoin de rappels sur les bases de Seconde, regarde ces vidéos sur la pente et les équations cartésiennes.

Un exercice classique mêlant vecteurs directeurs et droites parallèles. Tu peux tout de suite retenir que droites parallèles signifie droites :
- de même pente
- avec des vecteurs directeurs colinéaires

Dans cette exercice, les droites se coupent. Il faut donc résoudre des systèmes. Si tu es un peu rouillé à ce sujet, prends le temps de revoir ce chapitre de Seconde trop souvent mal maîtrisé

Un problème plus difficile pour finir étudiant une famille de droites.
On étudie pour cela une équation paramètrée.
En général, ce genre d'exercice vous fait peur. Mais pas de panique avec un peu de méthode, c'est faisable... On explique d'abord comment marche une équation avec paramètre puis on voit les clefs pour résoudre ce genre de problème.
En cours de route on tombe sur des équations de degré 2. Si tu as oublié les méthodes pour trouver les racines regarde ces vidéos :
- Racines et tableau de signes 1.
- Racines et tableau de signes 2.
Si tu ne connaissais pas encore : la technique de l'indien.