




Assez simple
01 Les vecteurs
On examine les mouvements d'un personnage dans un jeu vidéo pour comprendre ce qu'est un vecteur et comment le décrire ?
On voit au passage l'incontournable relation de Chasles.
Présentation des vecteurs, techniques de tracé, théorème de Chasles, parallélogramme et milieu.
Tout ce qu'on peut faire avec les vecteurs sans coordonnées.





Assez simple
On examine les mouvements d'un personnage dans un jeu vidéo pour comprendre ce qu'est un vecteur et comment le décrire ?
On voit au passage l'incontournable relation de Chasles.




Assez simple
Tu as un vecteur et on te demande de tracer un deuxième vecteur égal au premier uniquement à la règle et au compas.
Pas très marrant et un peu d'un autre temps, on est d'accord...
Si ton professeur t'a appris comment le faire et que ça ne t'inspire pas
regarde cette vidéo car il pourrait te le demander lors du premier devoir sur les vecteurs.
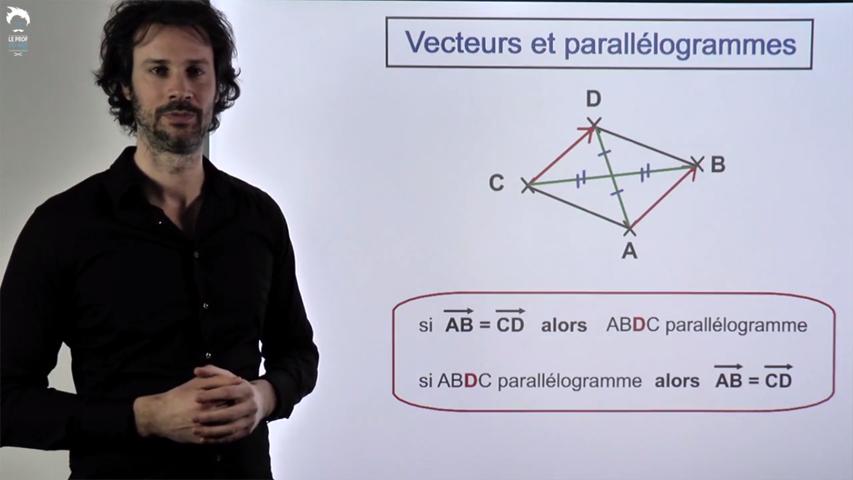
Retiens surtout pour la suite le lien essentiel entre vecteurs et parallélogramme
qui te servira souvent dans les problèmes.





Assez simple
C'est facile... Ok.
Mais méfiance tout de même car il y a des situations où bien l'appliquer
est subtil voire très subtil...
Une vidéo incontournable avant un DS.





Assez simple
Des bases qui te serviront tout au long du chapitre
Bonne nouvelle, on a jeté le compas...





D'un bon niveau
Derrière certaines formules qui contiennent des vecteurs se cachent un milieu.
On voit comment les trouver sans se fatiguer à les mémoriser.
Une vidéo "astuce" à voir une fois.





D'un bon niveau
La façon la plus efficace de décrire un vecteur ce sont ses coordonnées dans un repère.
On reconstruit ensemble cette formule et on voit comment l'utiliser.





Assez simple
La formule vue dans la précédente vidéo sert à calculer les coordonnées d'un vecteur mais pas seulement.
Elle permet aussi de trouver les coordonnées d'un point inconnu.
Une application à maîtriser absolument.
La colinéarité est souvent le coeur des problèmes sur les vecteurs.





Assez simple
Comment démontrer que des vecteurs sont colinéaires et à quoi ça sert ?
Une vidéo de présentation de tout ce qu'il faut savoir sur la colinéarité.
Remarque importante :
La plupart des professeurs vous présente la technique "des diagonales des coordonnées", car c'est une méthode simple et efficace.
Si ce n'est pas le cas de ton professeur demande lui s'il accepte que tu l'utilises.





D'un bon niveau
Cela se corse un peu.
On doit montrer que des vecteurs sont colinéaires mais cette fois on n'a plus de coordonnées !?
Deux exercices pour comprendre comment faire.





Assez simple
Deux droites sont elles parallèles ?
Trois points sont-ils alignés ?
Des questions que tu rencontras à coup sûr en DS.
Tout repose sur la colinéarité on va le voir.
A maîtriser sur le bout des doigts.





D'un bon niveau
Zoom sur un exercice type incontournable.
Savoir si deux vecteurs sont colinéaires ou non ?





D'un bon niveau
Dans les exercices sur la colinéarité, vous calez souvent au moment de trouver
le coefficient de proporitionalité entre les deux vecteurs.
Pourtant il existe une méthode expéditive qui permet de le trouver très rapidement...
Un point méthode indispensable pour réussir dans ce chapitre.
Une série de problèmes sur les vecteurs pour t'entraîner avant un devoir.





D'un bon niveau
Un premier problème sur les vecteurs comme tu peux en avoir en DS





D'un bon niveau
Deuxième problème sur les vecteurs pour t'entrainer.
Bilan sur l'essentiel du chapitre sur les vecteurs d'abord.
Incontournable !
Enfin, un rappel des formules essentielles avec des coordonnées.
A voir absolument si tu as déjà eu le cours de géométrie analytique (formules milieu et longueur...) car ces formules pourraient alors apparaitre dans ton devoir sur les vecteurs...





Assez simple
L'essentiel de ce qu'il faut savoir et savoir faire avec des vecteurs en Seconde.





D'un bon niveau
Quand on a les coordonnées de deux points on peut calculer : milieu, longueur mais on peut aussi calculer les coordonnées d'un vecteur et la pente d'une droite.
Bilan des quatre grandes formules de géométrie qu'il faut connaître quand vous avez un repère pour résoudre tous les problèmes !