Résultat de la recherche pour "hypothèse par récurrence"

Vidéos

Raisonnement par récurrence Vip 10 min 28 s

01 Raisonnement par récurrence

Mots(s) trouvé(s): récurrence Terminale > Suites - Le raisonnement par récurrence et les limites
Mickaël 10 min 28 s

Je commence par t’expliquer rapidement ce qu’est une démonstration par récurrence.
On se concentre ensuite sur l’hérédité, le passage le plus délicat d’une démonstration par récurrence.
De nombreux conseils et une méthode simple et efficace pour ne plus coincer sur cet exercice incontournable.
Modélisation d'une suite Vip 3 min 9 s

01 Modélisation d'une suite

Mots(s) trouvé(s): récurrence Première > Les suites numériques
Mickaël 3 min 9 s

On voit comment bien démarrer sur un exercice où la suite, ni arithmétique, ni géométrique, est définie par un texte.
On voit:
- comment traduire ce texte en formule mathématique
- comment calculer les premiers termes de la suite
- comment trouver sa définition par récurrence.
Une fois ces bases comprises passent au problème suivant.
Un classique de fin de chapitre et de Terminale que tu as de bonnes chances d'avoir en DS.

Généralités sur les suites : suites quelconques Vip 7 min 23 s

01 Généralités sur les suites : suites quelconques

Mots(s) trouvé(s): récurrence Première > Les suites numériques
Mickaël 7 min 23 s

Quand une suite n'est pas arithmétique ou géométrique le plus important pour commencer est de regarder comment cette suite est définie.
Si elle est définie en fonction de n (définition explicite) les techniques pour l'étudier sont très simples et exposées ici.
Elles seront plus subtiles si la suite est définie par récurrence...
Si tu veux voir comment tracer une suite définie par récurrence regarde le début de ce problème : étude d'une suite homographique.

Problème : étude d'une suite homographique Vip 9 min 16 s

01 Problème : étude d'une suite homographique

Mots(s) trouvé(s): récurrence Terminale > Suites - Le raisonnement par récurrence et les limites
Mickaël 9 min 16 s

Une suite définie par récurrence est étudiée par l’intermédiaire de la fonction associée.
Pas facile de comprendre ce que ça veut dire à la première lecture…
Mais interdiction de partir en courant car la moitié des problèmes de suite sont de ce type, alors prends le temps de regarder cette vidéo pour savoir ce qui t’attend en DS ou au Bac.
- toutes les clefs pour réussir ces classiques du Bac
- en prime quelques astuces.
Une vidéo qui peut te faire gagner à elle toute seule quatre ou cinq points !
Remarques : si tu ne comprends pas pourquoi on doit justifier que la fonction est croissante dans les hérédités, regarde cette vidéo.
Et si tu as des difficultés à retourner la relation entre Un et Vn, tu peux t’entrainer avec cette vidéo.

Démonstration utilisant un raisonnement par récurrence Vip 3 min 33 s

01 Démonstration utilisant un raisonnement par récurrence

Mots(s) trouvé(s): récurrence Terminale > Suites - Le raisonnement par récurrence et les limites
Mickaël 3 min 33 s

Dernière démonstration au programme officiel sur les suites. De niveau Terminale, enfin !
Elle s’appuie sur un raisonnement par récurrence. Un bon entraînement pour étudier ce point de cours.
Si tu veux la refaire seul, note bien les clefs pour démarrer, elles ne sont pas évidentes à trouver.

Suites géométriques: définition par récurrence et explicite Vip 6 min 24 s

01 Suites géométriques: définition par récurrence et explicite

Mots(s) trouvé(s): récurrence Première > Les suites numériques
Mickaël 6 min 24 s

On découvre ce qu'est une suite géométrique puis on se donne les mêmes objectifs que dans la vidéo précédente.
- Trouver un terme d'indice donné.
- Donner sa définition par récurrence.
- En déduire sa définition explicite.
Des bases incontournables!

Raisonnement par récurrence Vip 10 min 28 s

01 Raisonnement par récurrence

Mots(s) trouvé(s): récurrence Terminale > Suites - Le raisonnement par récurrence et les limites
Mickaël 10 min 28 s

Si une propriété est vraie pour un entier petit, 1 par exemple, et que tu démontres qu’elle se transmet d’un entier au suivant alors elle sera vraie pour 2 puis pour 3, 4… et donc pour tous les entiers. C’est le principe de récurrence. Plus dur, l’hérédité? Ca consiste à démontrer que la propriété se transmet. C’est sur cette difficulté que se concentre cette vidéo de méthode où je te montre comment t’organiser pour voir clairement ce que tu cherches à prouver et le trouver ! Incontournable.
Un modèle renforcé et efficace : sédiments marins et données GPS Vip 6 min 18 s

01 Un modèle renforcé et efficace : sédiments marins et données GPS

Mots(s) trouvé(s): hypothèse Première > Renforcement et évolution du modèle de la tectonique des plaques
Jean-Patrice 6 min 18 s

Dans cette vidéo, on verra comment les sédiments marins confirment l'âge de la croûte océanique.
L'étude des données GPS valide cette hypothèse.

L’hypothèse d’une expansion océanique Vip 5 min 5 s

01 L’hypothèse d’une expansion océanique

Mots(s) trouvé(s): hypothèse Première > Naissance d'un modèle global, la tectonique des plaques
Jean-Patrice 5 min 5 s

L'étude de la topographie océanique, l'observation de la chaleur interne du globe à sa surface,
l'étude du plancher océanique et la mesure d'anomalies magnétiques dans ses roches...
Autant d'indices qui soutiennent l'hypothèse d'une expansion océanique.
Remise en cause du modèle néoclassique Vip 4 min 1 s

01 Remise en cause du modèle néoclassique

Mots(s) trouvé(s): hypothèse Terminale > Marché du travail et Gestion de l'emploi
Nathalie 4 min 1 s

Le modèle néoclassique du marché du travail s’appuie sur les hypothèses du modèle de concurrence pure et parfaite alors que dans la réalité les hypothèses sont rarement vérifiées. Dans ce cas, c’est l’intégralité du modèle qui va être remis en cause.
Définition par récurrence et définition explicite - Suites arithmétiques et géométriques Free 9 min 5 s

01 Définition par récurrence et définition explicite - Suites arithmétiques et géométriques

Mots(s) trouvé(s): récurrence Terminale > Avec les suites arithmétiques et géométriques
Mickaël 9 min 5 s

Une vidéo pour avoir les idées claires et partir sur du solide. À voir absolument !
On fait d’abord un rappel sur les deux façons de décrire des suites :
- définition par récurrence et définition explicite.
Je te montre ensuite comment reconstruire très simplement les définitions par récurrence et explicite des suites arithmétiques et géométriques.
Un bon moyen de retrouver des formules qui te serviront à longueur de temps dans les problèmes.
Suites arithmétiques: définition par récurrence et explicite Vip 7 min 53 s

01 Suites arithmétiques: définition par récurrence et explicite

Mots(s) trouvé(s): récurrence Première > Les suites numériques
Mickaël 7 min 53 s

On présente une suite arithmétique dont on essaye de trouver le 101ème terme.
Pour cela on construit successivement sa "définition par récurrence" et sa "définition explicite".
On effectue le même travail sur un deuxième exemple avant d'exposer des formules générales valables pour toutes les suites arithmétiques.
Nous en profitons pour expliquer le vocabulaire rattaché aux suites et une méthode pour les représenter simplement.

Démonstration par récurrence appliquée aux suites Vip 3 min 39 s

01 Démonstration par récurrence appliquée aux suites

Mots(s) trouvé(s): récurrence Terminale > Suites - Le raisonnement par récurrence et les limites
Mickaël 3 min 39 s

Démonstration par récurrence – sur une Suite – Méthode
La démonstration de l’hérédité quand on a affaire à une Suite peut se faire vite voire très vite…
à condition de connaitre les deux techniques qui s’appliquent spécialement aux Suites.
- Reconstruire étape par étape le terme n+1.
- Appliquer f.
On voit comment appliquer chacune de ces méthodes.
Puis comment choisir la bonne dans un problème.
Une vidéo de méthode incontournable aussi importante qu’une formule de cours !

Continuité et théorème des valeurs intermédiaires Free 5 min 55 s

01 Continuité et théorème des valeurs intermédiaires

Mots(s) trouvé(s): hypothèse Terminale > Continuité et Théorème des Valeurs Intermédiaires
Mickaël 5 min 55 s

On voit d’abord ce qu’est une fonction continue.
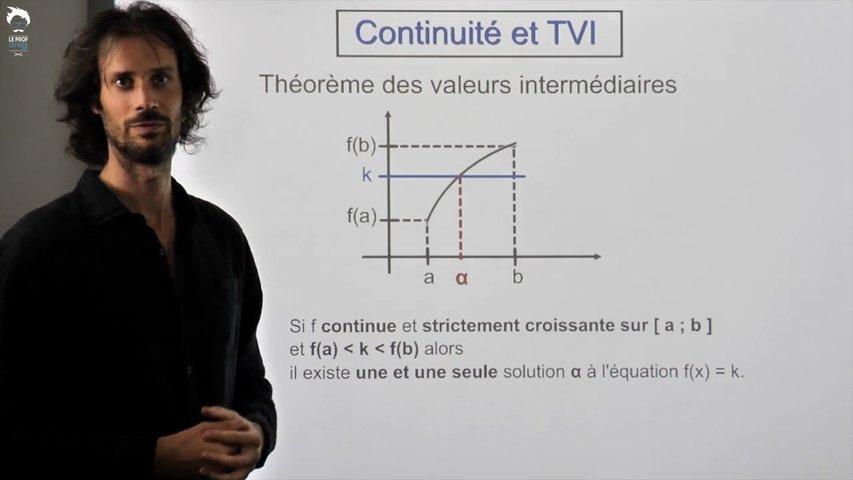
Puis on se concentre sur le Théorème des Valeurs Intermédiaires, un théorème très intuitif.
La seule difficulté : il faut bien penser à rappeler les trois hypothèses qui permettent de l’utiliser.

Chapitres

  1. Suites - Le raisonnement par récurrence et les limites (terminale/S/SI)
  2. Suites - Le raisonnement par récurrence et les limites (terminale/réforme 2019)