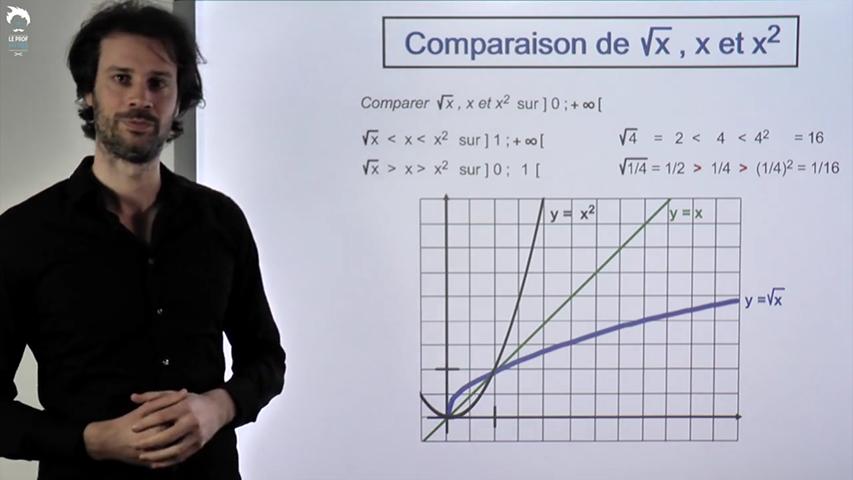
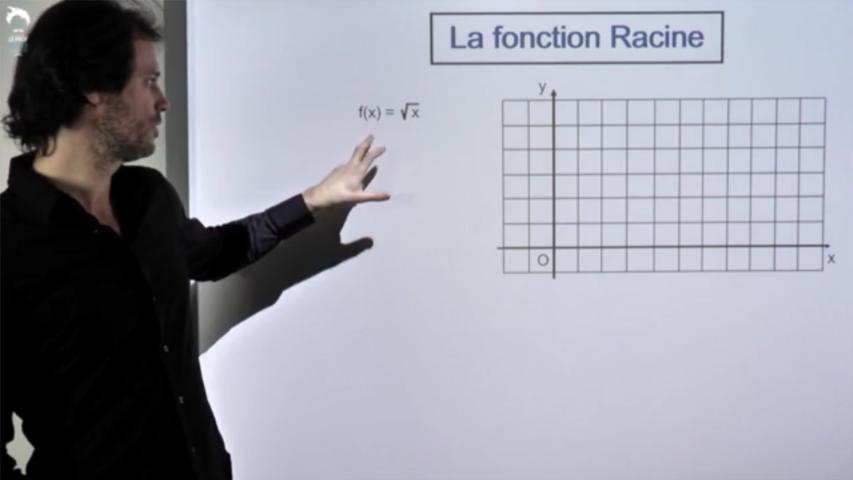
Facile à tracer, ses tableaux de signes et de variations sont ultra-simples.
Attention par contre à son ensemble de définition et aux équations où elle apparait.
Retenez pour le long terme ce qu'est la quantité conjuguée. Un outil qui vous servira de temps à autres pour décoincer un exercice difficile.
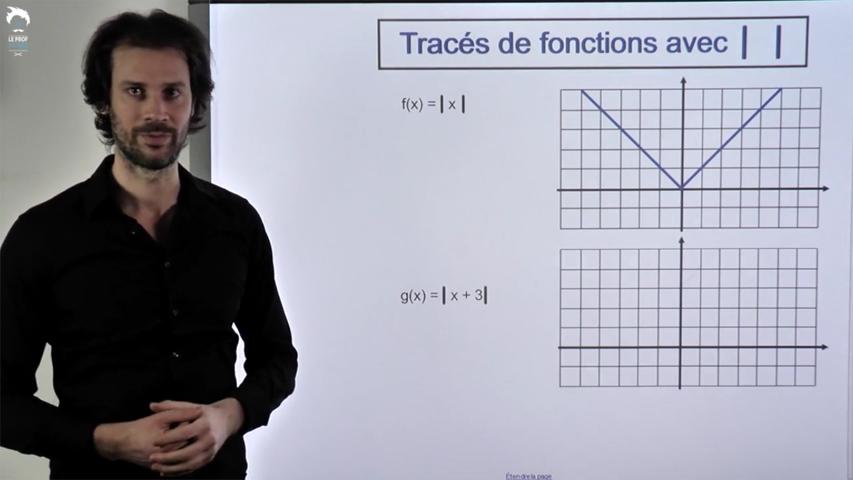
La fonction "tueuse" de négatifs qui traduit des distances...
Une fonction que vous croiserez aussi en Physique cette année.
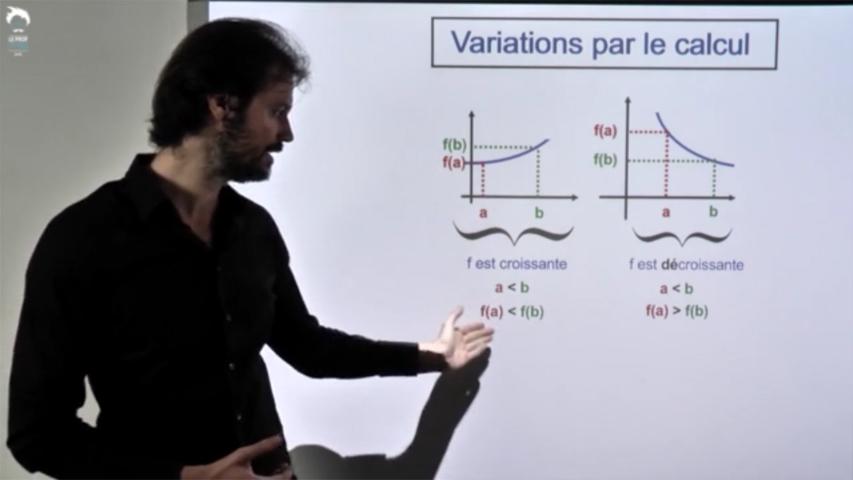
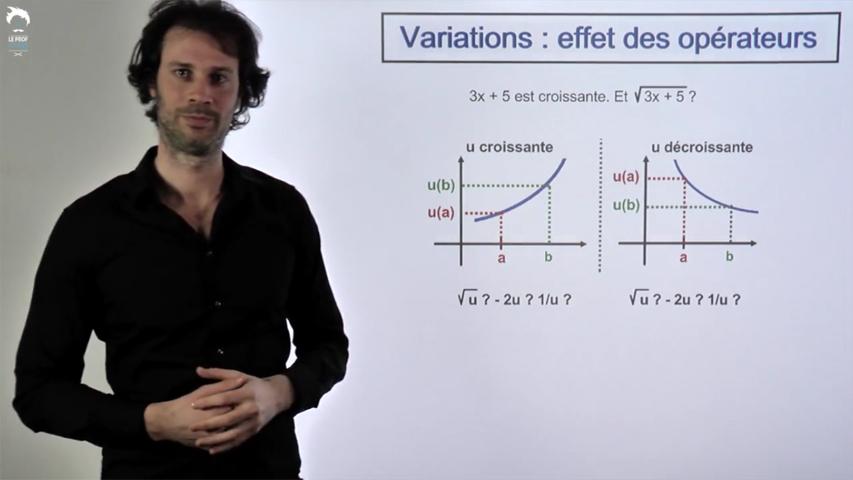
La première est une vieille connaissance que vous avez croisée lors de plusieurs démonstration de Seconde ou début Première. a < b Que dire de f(a) et f(b) ?...
Une approche de la croissance qui vous sera encore utile en Terminale.
Une deuxième méthode simple à comprendre mais très lourde à utiliser que vous vous empresserez d'oublier, dès que vous aurez appris la dérivation (chapitre suivant).
Mais à ne pas négliger pour un DS sur ce chapitre! Un exercice fétiche de beaucoup de professeurs pour le DS sur cette leçon...