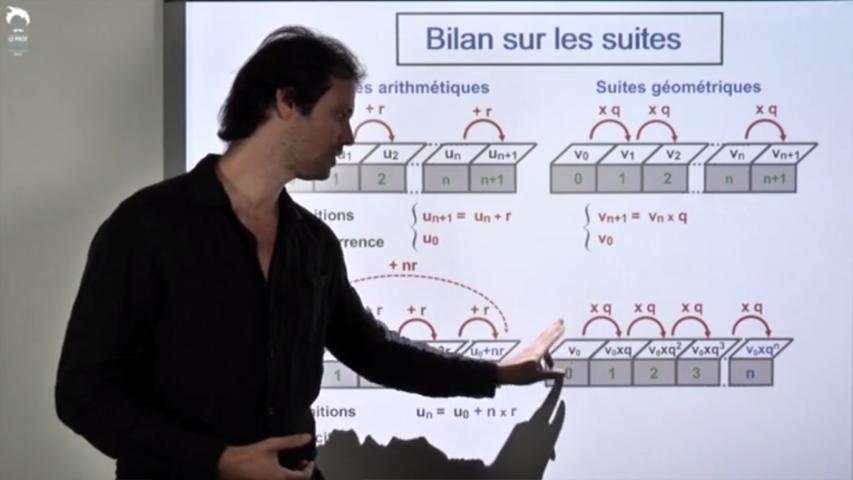
Nous verrons:
- Leurs définitions par récurrence et explicite (vidéos 1 et 2).
- Comment démontrer qu'une suite n'est pas arithmétique ou n'est pas géométrique (vidéo 3)
- Comment déterminer leurs caractéristiques avec seulement deux termes (vidéo 3)
- Leurs comportements: variations et limites (vidéo 4)
Ici on retrouve une série de problèmes classiques sur les suites arithmétiques et géométriques tels que vous pourrez en rencontrer en DS ou DM.
On présente ici quelques suites qui ne sont ni arithmétiques ni géométriques et on voit les méthodes les plus simples pour les étudier.