




Très facile
01 La dérivation : À quoi ça sert ?
La dérivation : qu'est ce que c'est ? Pourquoi est-elle si importante ? À travers des exemples concrets on voit ensemble à quelles questions essentielles la dérivation apporte des réponses.
Une première partie où l'on explique concrètement ce qu'est la dérivation avant de construire les premières formules de la leçon.
On commence par une vidéo incontournable pour comprendre vraiment à quoi sert la dérivation.
Ensuite, on enchaîne sur deux vidéos qui se concentrent sur les formules de cours.
Enfin, on s'entraîne utiliser toutes ces formules. On calcule des "nombres dérivées" ou "dérivées en un point" en passant par la formule du "taux d'accroissement". On les utilise pour calculer des équations de tangente.





Très facile
La dérivation : qu'est ce que c'est ? Pourquoi est-elle si importante ? À travers des exemples concrets on voit ensemble à quelles questions essentielles la dérivation apporte des réponses.





Assez simple
On a vu dans la vidéo précédente que la dérivée est liée à la notion de pente. Mais comment calculer précisément la pente d'une courbe autrement dit d'une "ligne qui tourne" ? On découvre en chemin le taux d'accroissement et la notion de tangente.




Assez simple
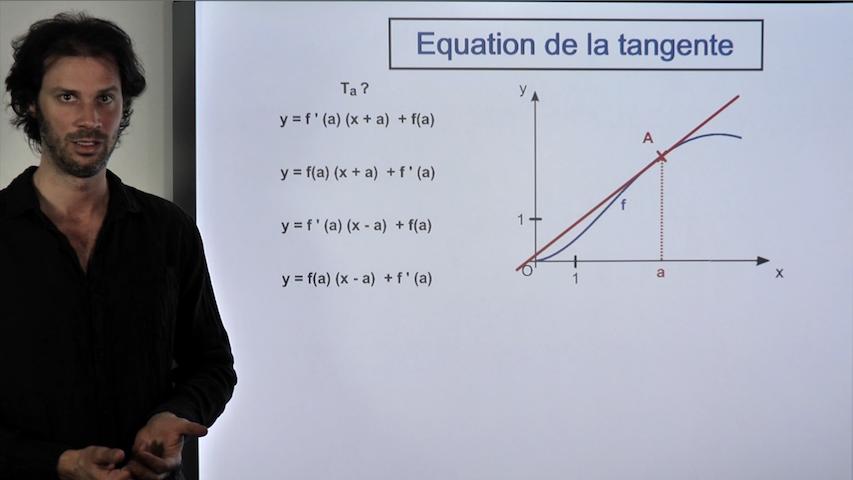
On démontre une formule clef de ce chapitre: l'équation d'une tangente
On part d'un dessin qui nous aide à faire et comprendre la démonstration.
Une fois la formule obtenue je te donne des astuces pour la retenir
sans en mélanger les éléments.





Assez simple
Un exercice type de début de leçon sur lequel tu seras sûrement interrogé lors de ton premier test sur la dérivation.
Les exercices de début de leçon sont souvent simples et rapides.
Ici, c'est tout le contraire : répétitif et calculatoire…
On va dire que c’est l’occasion de revoir les principales techniques de transformation des expressions :
- identités remarquables
- factorisation
- mise au même dénominateur
Un exercice technique à maîtriser pour réussir son premier DS sur la dérivation.
On vient de voir que calculer la dérivée avec le taux d'accroissement est long et lourd.
On apprend ici à calculer des dérivées avec une nouvelle méthode basée sur les formules de dérivation. On utilise une dernière fois le taux d'accroissement pour démontrer ces nouvelles formules (première vidéo) puis on découvre une liste de formules à apprendre par coeur.
Je te donne comme d'habitude des astuces pour les mémoriser
et on apprend à les utiliser efficacement.





D'un bon niveau
Cette fois on doit construire le tableau de variations de fonctions quotients. Un grand classique des DS sur la dérivation. Attention à l'ensemble de définition !





Assez simple
Si on veut la dérivée d'une fonction en différents points, il est inutile de recalculer à chaque fois le taux d'accroissement.
Pourquoi ? Parce qu'on peut calculer une fois pour toute une formule !
Mieux on va mémoriser cette formule pour ne plus avoir à la recalculer !
Bref, à partir de maintenant on ne calculera plus des dérivées en un point mais des fonctions dérivées.
On démontre ici les formules des fonctions dérivées des fonctions « carré », « inverse » et « racine ».
Trois démos souvent à restituer en devoir.





Assez simple
Les formules de dérivation sont à connaître sur le bout des doigts. Elles sont un peu les tables de multiplication de la Terminale.
On voit ici comment les retrouver, les mémoriser et les utiliser efficacement.
Une vidéo à voir et revoir !
Si tu ne te sens pas à l'aise avec les puissances, regarde cette vidéo : mise au point sur les puissances.





D'un bon niveau
Deux formules pour gagner du temps d'abord, puis une série de formules qui te permettront de dériver n'importe quelle fonction !
Je te montre une technique très pratique pour toutes les mémoriser d'un coup !
Une méthode qui vaut le détour…
Attention ! Les formules de cette seconde partie de la vidéo sont à la limite du programme.
Elles ne sont pas toujours présentées en Première.





D'un bon niveau
Savoir calculer des fonctions dérivées, c'est la base pour réussir les exercices et problèmes de ce chapitre.
Une série d'exemples pour maitriser cette étape incontournable, éviter les erreurs et gagner du temps.
Une vidéo à voir absolument.





D'un bon niveau
On construit le tableau de variations d'un polynôme de degré 2 puis on calcule les équations de deux de ses tangentes.
On voit enfin comment utiliser les tangentes pour faire un tracé précis de la courbe.
Un exercice classique à maîtriser absolument !
En cas de difficultés je te propose trois vidéos :
Une vidéo pour savoir comment trouver le signe d'une fonction affine.
Une autre pour comprendre la formule qui donne l'équation d'une tangente.
Et une troisième pour réussir ses tracés de droite.





D'un bon niveau
On monte d'un petit cran en difficultés avec le tableau de variations d'un polynôme de degré 3. Il faut se souvenir de la méthode pour trouver le signe d'un polynôme de degré... 2 !
En cas de doute à ce sujet, regarde ces deux vidéos :
- Racines et tableaux de signes d'un polynôme 1
- Racines et tableaux de signes d'un polynôme 2
Et si tu ne connais pas la "technique de l'indien", elle est expliquée ici
Technique de l'indien
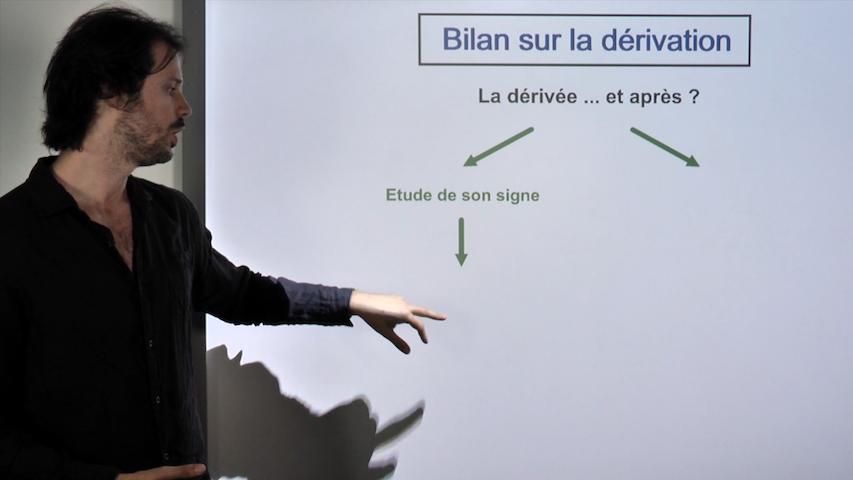
Une synthèse de l'essentiel du chapitre pour mettre tes idées au clair avant d'attaquer les problèmes.
On revoit les formules à connaître, quand et comment les utiliser
ainsi que les pièges à éviter.




D'un bon niveau
Taux d'accroissement, tangente, formules de dérivations. On passe en revue toutes les formules clefs de ce chapitre. On rappelle quand et comment les utiliser et on fait le point sur ce qui sert concrètement dans les exercices et les problèmes
Deux problèmes d'optimisation pour commencer: l'optimisation est un exercice type incontournable que tu auras forcément en devoir...
Deux exercices d'interprétation graphique ensuite qui surprennent beaucoup d'élèves. Ne manque surtout pas cette vidéo pour que ce ne soit pas ton cas.
Enfin, un problème avec des tangentes où les questions sont de moins en moins évidentes... Un bon moyen de peaufiner ta maitrise de ce chapitre une fois que tu as des bases solides.
Une série exercices que tu devras affronter en DS
et que tu recroiseras aussi en Terminale et probablement au bac... Autrement dit, des exercices types qui méritent que tu y passes du temps.





D'un bon niveau
Une série exercices que tu devras affronter en DS
et que tu recroiseras aussi en Terminale et probablement au bac...
Autrement dit, des exercices types qui méritent que tu y passes du temps.
Ici on cherche à optimiser les bénéfices d'un atelier de production c'est-à-dire pour quel nombre de pièces produites le bénéfice devrait être maximum.
La clef : construire le tableau de variations de la fonction bénéfice.





Difficile
Tu dois d'abord calculer une tangente en une abscisse donnée (la question "basique" sur les tangentes), puis les choses se corsent:
Tu dois trouver une tangente parallèle à une droite donnée.
Enfin, tu dois trouver le point d'intersection de deux tangentes.
En cas de doute sur la formule de la tangente vois ou revois la vidéo sur l'équation de la tangente




Assez simple
Deux exercices classiques au bac où la dérivée ne sert pas à construire un tableau de variation.
Regarde cette vidéo de méthode pour ne pas te faire surprendre par ces questions un peu inhabituelles.
Il s’agit de :
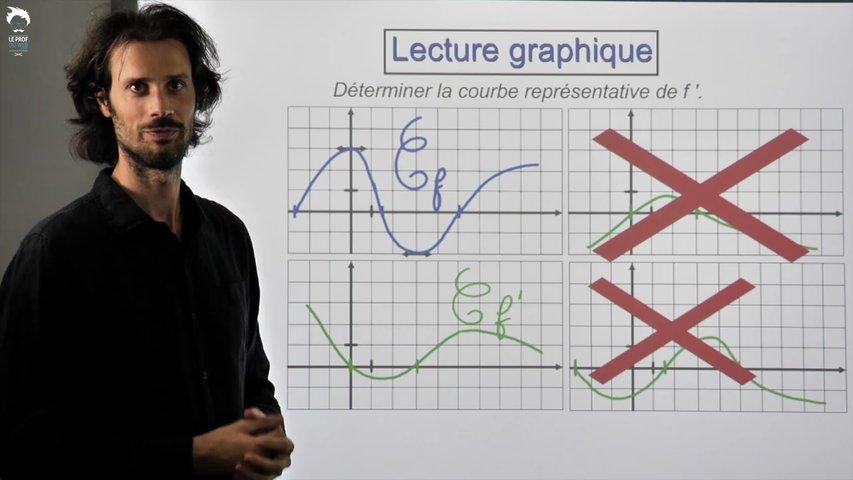
- Trouver l’expression d’une fonction à partir d’informations sur sa courbe.
- Toujours à partir d’une courbe trouver la courbe de la dérivée parmi plusieurs courbes au choix.
Un classique des QCM.
Tu peux te préparer aux interprétations graphiques en regardant cette série de vidéos :
La dérivation : à quoi ça sert ?
Dérivée en un point, taux d'accroissement et tangente
Que faire quand la pente d'une droite ne tombe pas juste ?