




Assez simple
01 Les bases des probabilités - 3/3 UNION – INTERSECTION – P(AUB) - BILAN
Pour finir les rappels, on fait des tirages très instructifs dans une urne.
Les bases de probabilités que vous avez croisées au collège ou en seconde et souvent oubliées.
Trois vidéos pour se remettre dans le bain
revoir les méthodes clefs
et faire un premier plein d'astuces utiles pour les exos.





Assez simple
Pour finir les rappels, on fait des tirages très instructifs dans une urne.





Assez simple
A travers des expériences simples (jets de pièces ou de dés, tirages dans des urnes), on voit :
- le vocabulaire et les méthodes vus dans les classes précédentes
- quelques astuces à connaître et des réflexes à acquérir.
Première partie. On jette des pièces.





Assez simple
Deuxième partie de la vidéo.
Rappels basés sur l’observation d’expériences simples avec des dés.
L'espérance et la loi binomiale, vues en Première, sont indispensables pour finir les problèmes de Terminale.
Ces vidéos sont là pour te remettre au clair rapidement sur ces notions
et te montrer comment les utiliser dans les exercices.
Ne fais pas l'impasse sur la vidéo sur les combinaisons
si tu prépares un concours où la calculatrice est interdite.





D'un bon niveau
Un exercice assez subtil mêlant la loi binomiale et différentes façons de calculer l’espérance.
À maitriser pour se donner toutes les chances d’aller chercher les derniers points des problèmes de probabilités.





Assez simple
Des combinaisons apparaissent dans la formule de la loi binomiale.
Une vidéo pratique qui t'aidera à mieux comprendre et maitriser les combinaisons.
Incontournable pour ceux qui passent des concours où la calculatrice est interdite.





Assez simple
Est-ce que ça vaut le coup d’investir dans une carte d’abonnement pour avoir des réductions sur des trajets en train ?
Un problème pour vérifier que tu sais calculer l’espérance d’une variable aléatoire et l’interpréter.





Très facile
Si tu sais calculer une moyenne, tu sauras calculer une espérance.
Cette vidéo t'explique pourquoi.
On verra aussi ce que signifie un « gain algébrique ».
Deux notions indispensables pour les DS et le Bac.





D'un bon niveau
On jette un dé trois fois, dix fois, n fois et on voit apparaître petit à petit une formule
dont l’application dépasse largement les jets de dés.
C’est la loi binomiale.
Une des lois les plus importantes de l’univers des probabilités.
- On reconstruit d’abord la formule pour la comprendre et faciliter sa mémorisation.
- On voit ensuite son espérance, sa variance et ses conditions d’applications.
Probabilités conditionnelles et indépendance sont les deux seules nouveautés de Terminale.
Elles donnent lieu à des problèmes stéréotypés que tu dois maîtriser les yeux fermés.
Des points facile à prendre en devoir ou au bac.
Une première vidéo t’explique rapidement les formules de cours
Puis je te présente deux exercices types avec des astuces pour être rapide et efficace.
IMPORTANT : le test d’indépendance est hors programme pour les terminale ES, mais c’est une question
courante dans les concours des écoles de commerce qui recrutent au niveau Terminale,
raison pour laquelle je vous l'ai présenté.





Difficile
En observant un tirage dans une urne,
on reconstruit en quelques secondes les formules de probabilités conditionnelles
et dans la foulée la formule qui permet de tester l’indépendance de deux évènements
D’une pierre deux coups…
Et pour toi un excellent moyen de revoir ou retrouver rapidement ces formules incontournables.
Important : le test d’indépendance est hors programme pour les terminale ES,
mais c’est une question courante dans les concours
des écoles de commerce qui recrutent au niveau Terminale.





Assez simple
Tout simplement le cœur des exercices de probabilités conditionnelles, passé à la loupe pour que tu ne perdes pas un point et une seconde sur ce chapitre.
Un exercice de référence à voir absolument pour être sûr d’être efficace du début à la fin, et d’avoir une rédaction qui tient la route.





Assez simple
Est-ce que ceux qui portent des lunettes réussissent mieux en maths ?
Une question qui semble une blague à laquelle un test d’indépendance apporte une réponse surprenante.
Et pour toi l’occasion de voir ou revoir comment déterminer si deux évènements sont indépendants.
Une série de problèmes pour s’entrainer.
Le test médical est un incontournable
que tu croiseras forcément à un moment ou un autre
en devoir, au bac blanc ou au bac.
La grande nouveauté ici,
c’est le problème qui mixte Probabilités et Suites.
Un classique pour les S, plutôt un exercice de DM pour les ES.





D'un bon niveau
Cette vidéo est la correction expliquée d’un exercice, retrouve le sujet ici.
C’est simple : si vous réussissez cet exercice vous maitrisez les trois principales notions des probabilités discrètes au bac :
- Espérance
- loi binomiale
- probabilités conditionnelles.
Un problème d’un bon niveau.





Difficile
Deux bacheliers.
Une discussion sur les chances de réussir à un concours.
Un exercice de probabilités conditionnelles subtil où il faut prendre des initiatives.
Un exercice difficile plutôt destiné aux élèves qui préparent les concours d’entrée
dans des écoles de commerce qui recrutent au niveau Terminale.





Assez simple
Cette vidéo est la correction expliquée d’un exercice, retrouve le sujet ici.
Le test médical, sans doute l’exercice le plus classique des probabilités conditionnelles.
A voir pour la méthode mais aussi pour la maitrise des pourcentages.
Comptez bien les zéros…





Difficile
Un grand classique pour les S...
Et pour les ES ?
Un exercice de DM probablement ou de DS si votre professeur place la barre haute pour votre classe.
A faire une fois que tu te sens très solides sur tout le reste.
Deux sujets de bac qui comportent des questions sur le chapitre des probabilités conditionnelles.





D'un bon niveau
Un problème d’assurance assez subtil qui traverse trois chapitres :
- Probabilités conditionnelles
- Probabilités continues
- Echantillonnage et estimation
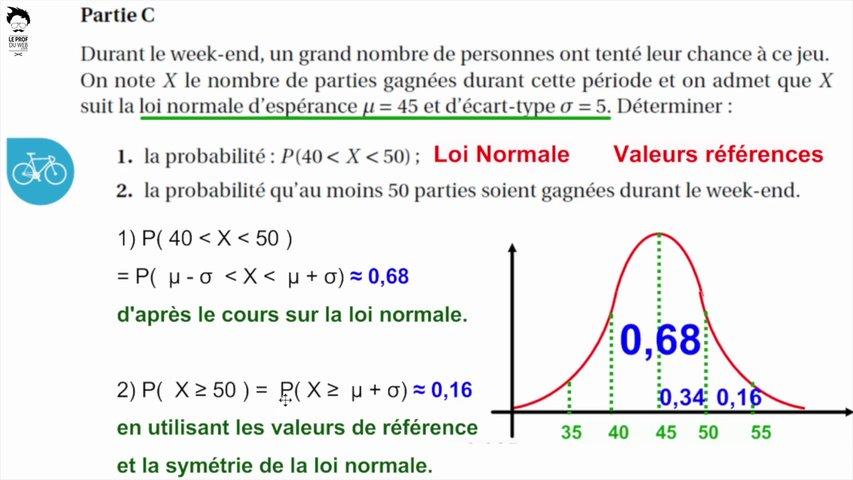




Assez simple
Un problème sur une roue de fête foraine
qui traverse les deux chapitres de probabilités.
Il commence avec des probabilités conditionnelles
puis bascule sur des probabilités continues.
Un exemple type de ce qui tombe souvent au bac.